Question

What is the perimeter of a regular pentagon with a side whose length is \[x + 4\] ?

Answer 1

Hint: Here in this question, we have to find the perimeter of a regular pentagon of given length \[l\] using a formula \[P = 5 \times l\] . If we are finding the perimeter of a regular pentagon, then we know that all five sides are equal lengths, so we can simplify the formula using multiplication operation to get the required solution.

Complete step-by-step answer:

In geometry, perimeter can be defined as the path or the boundary that surrounds a shape. It can also be defined as the length of the outline of a shape.
If a pentagon is regular, then all the sides are equal in length, and five angles are of equal measures
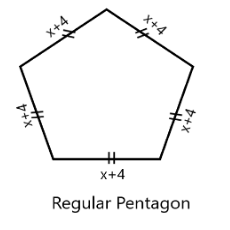
Consider a regular pentagon having length of \[x + 4\] , which is same for all sides of pentagon
The given regular pentagon has five equal sides. The perimeter is the distance around the outside of the pentagon. For a regular pentagon, the perimeter is the sum of the five sides or the length \[x + 4\] of a side multiplied by five.
 \[ \Rightarrow P = 5 \times l\]
 \[ \Rightarrow P = 5 \times \left( {x + 4} \right)\]
On multiplication, we get
 \[ \Rightarrow P = 5x + 20\]
Or the perimeter of regular pentagon can also find like
 \[ \Rightarrow P = l + l + l + l + l\]
 \[ \Rightarrow P = \left( {x + 4} \right) + \left( {x + 4} \right) + \left( {x + 4} \right) + \left( {x + 4} \right) + \left( {x + 4} \right)\]
 \[ \Rightarrow P = x + 4 + x + 4 + x + 4 + x + 4 + x + 4\]
On simplification, we get
 \[ \Rightarrow P = 5x + 20\]
Hence, the perimeter of a regular pentagon is \[5x + 20\] .
So, the correct answer is “ \[5x + 20\] ”.

Note: While determining the perimeter we use the formula. The unit for the perimeter will be the same as the unit of the length of a side or polygon. Whereas the unit for the area will be the square of the unit of the length of a polygon. We should not forget to write the unit with a final answer and we should also know about regular and irregular polygons.