Question

\[PQ\] is a double ordinate of hyperbola \[\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\] such that \[OPQ\] is an equilateral triangle, \[O\] being the centre of hyperbola, where eccentricity of hyperbola \[e\] satisfy \[\sqrt 3 e > k\], then the value of \[k\] is

Answer 1

Hint: Here, we will draw a figure that will satisfy the given condition. Then, using the properties of double ordinate of hyperbola and an equilateral triangle, we will compare the two equations. Substituting the end product into the eccentricity of a hyperbola, we will get the required value of \[k\].

Complete step-by-step answer:
Let the coordinates of point \[P\] be \[\left( {h,k} \right)\].
We will draw a figure showing the given conditions such that \[OPQ\] is an equilateral triangle, \[O\] being the centre of hyperbola.

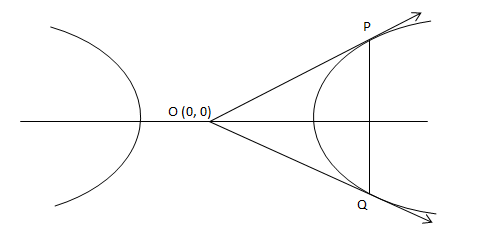
Since, \[PQ\] is a double ordinate of hyperbola, hence
\[l\left( {PQ} \right) = 2k\]
Also, \[l\left( {OP} \right) = \sqrt {{h^2} + {k^2}} \]
Now, according to the question, \[OPQ\] is an equilateral triangle. Hence,
\[2k = \sqrt {{h^2} + {k^2}} \]
Squaring both sides, we get
\[ \Rightarrow 4{k^2} = {h^2} + {k^2}\]
\[ \Rightarrow 3{k^2} = {h^2}\]…………………………….\[\left( 1 \right)\]
Now, point \[P\] lies on the hyperbola, so, it would satisfy \[\dfrac{{{h^2}}}{{{a^2}}} - \dfrac{{{k^2}}}{{{b^2}}} = 1\]………………….\[\left( 2 \right)\]
Substituting the value of equation \[\left( 1 \right)\] in equation \[\left( 2 \right)\], we get
\[\dfrac{{3{k^2}}}{{{a^2}}} - \dfrac{{{k^2}}}{{{b^2}}} = 1\]
\[ \Rightarrow {k^2}\left( {\dfrac{3}{{{a^2}}} - \dfrac{1}{{{b^2}}}} \right) = 1\]
Dividing both sides by \[{k^2}\], we get
\[ \Rightarrow \left( {\dfrac{3}{{{a^2}}} - \dfrac{1}{{{b^2}}}} \right) = \dfrac{1}{{{k^2}}} > 0\]
This is because \[{k^2}\] can neither be 1 nor be negative.
Hence, the above equation can be written as:
\[\dfrac{{{b^2}}}{{{a^2}}} > \dfrac{1}{3}\]
Now, we know that, \[{e^2} = 1 + \dfrac{{{b^2}}}{{{a^2}}} > 1 + \dfrac{1}{3} > \dfrac{4}{3}\], where \[e\] is the eccentricity.
Taking square root on both sides, we get
\[ \Rightarrow e > \dfrac{2}{{\sqrt 3 }}\]
Now, according to the question, the eccentricity of hyperbola \[e\] satisfies, \[\sqrt 3 e > k\]. So,
\[e > \dfrac{k}{{\sqrt 3 }}\]
Comparing \[e > \dfrac{k}{{\sqrt 3 }}\] and \[e > \dfrac{2}{{\sqrt 3 }}\], we can say that,
\[k = 2\]
Hence, this is the required answer.

Note: We can also solve this question using an alternate method:
Since, the points \[PQ\] lie on the hyperbola, so,
Coordinates of \[P = \left( {a\sec \theta ,b\tan \theta } \right)\]
Coordinates of \[Q = \left( {a\sec \theta , - b\tan \theta } \right)\]
Now, using distance formula, we get
\[PQ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
Substituting the values of coordinates, we get
\[ \Rightarrow PQ = \sqrt {{{\left( {a\sec \theta - a\sec \theta } \right)}^2} + {{\left( { - b\tan \theta - b\tan \theta } \right)}^2}} \]
Adding and subtracting the terms, we get
\[ \Rightarrow PQ = \sqrt {{{\left( { - 2b\tan \theta } \right)}^2}} = 2b\tan \theta \]
Similarly,
\[OQ = \sqrt {{{\left( {a\sec \theta - 0} \right)}^2} + {{\left( { - b\tan \theta - 0} \right)}^2}} \]
Adding the terms, we get
\[ \Rightarrow OQ = \sqrt {{a^2}{{\sec }^2}\theta + {b^2}{{\tan }^2}{\theta ^2}} \]
Since, \[OPQ\] is an equilateral triangle, hence,
\[PQ = OQ\]
\[ \Rightarrow 2b\tan \theta = \sqrt {{a^2}{{\sec }^2}\theta + {b^2}{{\tan }^2}{\theta ^2}} \]
Squaring both sides, we get
\[ \Rightarrow 4{b^2}{\tan ^2}\theta = {a^2}{\sec ^2}\theta + {b^2}{\tan ^2}{\theta ^2}\]
\[ \Rightarrow 3{b^2}{\tan ^2}\theta = {a^2}{\sec ^2}\theta \]……………………….\[\left( 3 \right)\]
Now, we know that in a hyperbola, \[{b^2} = {a^2}\left( {{e^2} - 1} \right)\].
Substituting \[{b^2} = {a^2}\left( {{e^2} - 1} \right)\] in equation \[\left( 3 \right)\], we get
\[ \Rightarrow 3{a^2}\left( {{e^2} - 1} \right){\tan ^2}\theta = {a^2}{\sec ^2}\theta \]
Substituting \[{\tan ^2}\theta = \dfrac{{{{\sin }^2}\theta }}{{{{\cos }^2}\theta }}\] and \[{\sec ^2}\theta = \dfrac{1}{{{{\cos }^2}\theta }}\], we get
\[ \Rightarrow 3\left( {{e^2} - 1} \right)\dfrac{{{{\sin }^2}\theta }}{{{{\cos }^2}\theta }} = \dfrac{1}{{{{\cos }^2}\theta }}\]
\[ \Rightarrow 3\left( {{e^2} - 1} \right){\sin ^2}\theta = 1\]
On cross multiplication, we get
\[ \Rightarrow {\sin ^2}\theta = \dfrac{1}{{3\left( {{e^2} - 1} \right)}}\]
The value of \[{\sin ^2}\theta \] is always less than 1, so
\[ \Rightarrow \dfrac{1}{{3\left( {{e^2} - 1} \right)}} < 1\]
Again on cross multiplication, we get
\[ \Rightarrow \dfrac{1}{{\left( {{e^2} - 1} \right)}} < 3\]
Taking reciprocal on both sides, and changing the inequality, we get
\[ \Rightarrow \left( {{e^2} - 1} \right) > \dfrac{1}{3}\]
Adding 1 on both sides, we get
\[ \Rightarrow {e^2} > \dfrac{1}{3} + 1 > \dfrac{4}{3}\]
Taking square root on both sides, we get
\[ \Rightarrow e > \dfrac{2}{{\sqrt 3 }}\]
Now, according to the question, the eccentricity of hyperbola \[e\] satisfies \[\sqrt 3 e > k\] or \[e > \dfrac{k}{{\sqrt 3 }}\].
Comparing \[e > \dfrac{k}{{\sqrt 3 }}\] and \[e > \dfrac{2}{{\sqrt 3 }}\], we can say that,
\[k = 2\]
 Hence, this is the required answer.