Question

PQ is a double ordinate of the parabola ${y^2} = 4ax$. If the normal at P intersects the line passing through Q and parallel to axis of x at G, then locus of G is a parabola with(More than one option correct)
(A). Length of latus rectum equal to 4a.
(B). Vertex at (4a,0).
(C). Directrix as the line x-3a=0
(D). Focus (5a,0)

Answer 1

Hint: Start by differentiating the equation of parabola w.r.t x and find out the slope of tangent and subsequently slope of Normal . Form the equation of Normal and find the intersection point with line passing through Q at G. Find the Locus by substituting values in parabola equation, and find other components as well. Draw a diagram for better understanding.

Complete step-by-step answer:

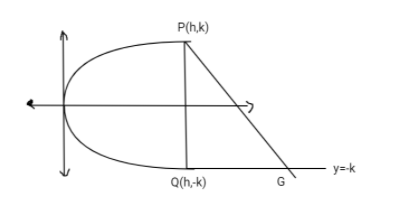
Given,
${y^2} = 4ax$
Differentiating w.r.t x , we get
$
  2y\dfrac{{dy}}{{dx}} = 4a \\
  2yy' = 4a \\
   \Rightarrow y' = \dfrac{{4a}}{{2y}} \\
$
Then slope at (h,k)
$ \Rightarrow y' = \dfrac{{2a}}{k}$
Now , we know that Normal is perpendicular to the tangent i.e. ${m_1} \cdot {m_2} = - 1$
$\therefore $Slope of normal ${\text{ = }}\dfrac{{ - 1}}{{{m_1}}}$
$
   \Rightarrow {m_2} = \dfrac{{ - 1}}{{\dfrac{{2a}}{k}}} \\
   \Rightarrow {m_2} = \dfrac{{ - k}}{{2a}} \\
$
Now, the equation of Normal passing through (h,k) will be
$y - k = \dfrac{{ - k}}{{2a}}(x - h)$
Cross multiplying 2a to the other side , we get
$2ay - 2ak = - kx + kh$
Putting $y = - k.$(as line passes through Q and intersect normal at G)
$
   - 2ak - 2ak + kx - kh = 0 \\
   - 4ak + kx - kh = 0 \\
$
Taking K common , we get
$
  k[ - 4a + x - h] = 0 \\
   \Rightarrow h = x - 4a \\
$
And we have $y = - k$
We know that (h,-k) lies on the parabola
$\therefore {k^2} = 4ah$
Substituting values of h and k , we get
${y^2} = 4a(x - 4a) \to locus$
So , the vertex = (4a,0)
Focus =(4a+a,0)=(5a,0)
Length of latus rectum = 4a
Directrix :${\text{ }}x = 4a - a$
$ \Rightarrow x = 3a{\text{ or }}x - 3a = 0$
The graph of locus would look like

Therefore , All the options are correct.

Note: All the properties and equations of different components of parabola and other graphs (Hyperbola, Ellipse, circle etc) must be known very well in order to solve such similar questions. Shifting of origin must be dealt carefully in the equations.