Question

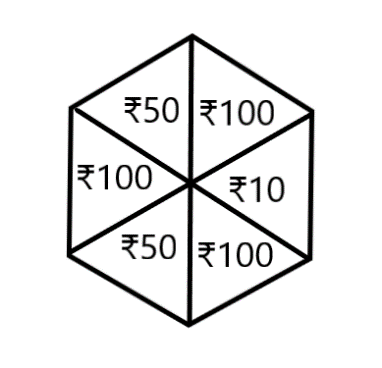
What is the probability of the spinner landing on${\text{Rs 100}}$
A.$\dfrac{1}{2}$
B.$\dfrac{1}{3}$
C.$\dfrac{1}{6}$
D.$\dfrac{5}{6}$

Answer 1

Hint: In order to find the probability of the spinner landing on ${\text{Rs 100}}$, find the total possible outcomes from the spinning wheel by counting all the values, then calculate the favourable outcomes that is the number of chances we can get ${\text{Rs 100}}$. Divide them to get the probability.
Formula used:
${\text{Probability = }}\dfrac{{{\text{Number of Favourable outcomes}}}}{{{\text{Number of Total possible favourable outcomes}}}}$

Complete answer:
We have a spinning wheel with some values of Rs written on it.
 

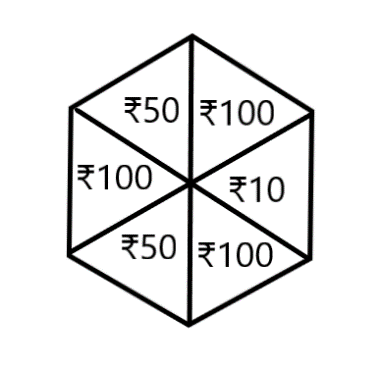
We need to find the probability of the spinner landing on ${\text{Rs 100}}$.For, that we need to find the possible outcomes and favourable outcomes.
We can see that there are a total of six values written on the spinner wheel, so any value can be obtained from this if the wheel is rotated.
So, total number of possible outcomes $ = 6$.
We need ${\text{Rs 100}}$, so there are three ${\text{Rs 100}}$, written on the spinning wheel, so when we rotate it, there are three chances of getting ${\text{Rs 100}}$.
Therefore, Number of Favourable outcomes $ = 3$
From the definition of Probability, we know that:
$\Rightarrow$ ${\text{Probability = }}\dfrac{{{\text{Number of Favourable outcomes}}}}{{{\text{Number of Total possible favourable outcomes}}}}$
Substituting the obtained value in it and, we get:
$\Rightarrow$ ${\text{Probability = }}\dfrac{3}{6}$
Simplifying it more, we get:
$\Rightarrow$ ${\text{Probability = }}\dfrac{1}{2}$
Hence, the probability of the spinner landing on ${\text{Rs 100}}$ is $\dfrac{1}{2}$, which is the option A.
Therefore, Option A is correct.

Note:
1.Probability is nothing but the number of favourable outcomes divided by the total number of possible outcomes. It is also written as ${\text{Probability = }}\dfrac{{N\left( E \right)}}{{N\left( S \right)}}$, where n(E) is the number of possible events and n(E) is the number of sample space.
2.Using the same method, we can find the probability of getting any other number on the spinning wheel.