Question

Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.

Answer 1

Hint: Here, we will assume that two concentric circles be C1 and C2 with centre O and the chord of the larger circle touches the smaller circle, then by making a figure and by using the condition that chord of larger circle is the tangent of smaller circle and also the perpendicular from the centre bisects the chord, we will get our required answer.

Complete step-by-step answer:
We need to prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
Let the two concentric circles be C1 and C2 with centre O. And let PQ be the chord of larger circle C1 which touches the smaller circle C2 at M.
Now, let us draw a figure using these information, we get

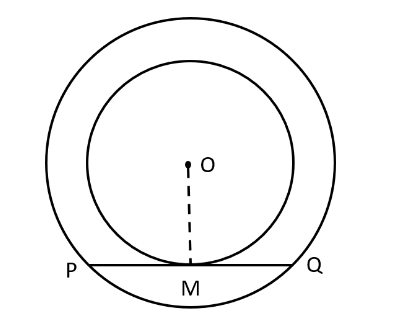
We need to prove that chord PQ is bisected at the point of contact M, i.e., \[PM{\text{ }} = {\text{ }}QM.\]
Here, in the figure, we can see that PQ is the tangent of smaller circle C2, then $OM \bot PQ.$
Now, PQ is the chord of the larger circle C1 and $OM \bot PQ.$
We know that, perpendicular from the centre bisects the chord. Therefore, OM will bisect the chord PQ.
\[ \Rightarrow PM{\text{ }} = {\text{ }}QM.\]
Hence proved, the chord of the larger circle is bisected at the point of contact.

Note: In the solutions, we have mentioned that the perpendicular from the centre bisects the chord. So, there is a chord theorem, according to that, in a circle, a radius which is perpendicular to a chord bisects the chord, whereas chord is the line segment that connects the two points in a curve, also the diameter is the longest chord of the circle.