Question

Prove that the area of a rhombus is equal to half the rectangle contained by its diagonals.

Answer 1

Hint: By the statement ‘rectangle contained by the diagonals’ refers to the rectangle the lengths of whose adjacent sides is equal to the length of the diagonals of the rhombus. We know that the area of the rhombus is equal to half the product of its diagonals while the area of the rectangle is equal to the product of the lengths of the adjacent sides.

Complete step-by-step answer:
Let us start the solution to the above question by drawing a rough, representative diagram of the situation given in the figure. The statement ‘rectangle contained by the diagonals’ refers to the rectangle the lengths of whose adjacent sides is equal to the length of the diagonals of the rhombus.

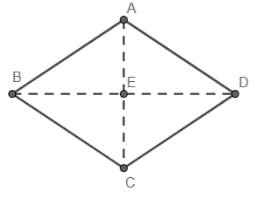
We know that the area of the rhombus is equal to half the product of its diagonals. So, the area of the rhombus ABCD is:
 $ ar(ABCD)=\dfrac{1}{2}\times AC\times BD $
Now, we know that the area of the rectangle is equal to the product of the lengths of the adjacent sides. Also, as it is given that the rectangle is contained by the diagonals, so the length of the adjacent sides is equal to AC and BD. So, the area of the rectangle is $ AC\times BD $ . If we put this in the area of the rhombus, we get
 $ \text{ar(ABCD)=}\dfrac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ }\left( \text{the area rectangle contained by its diagonals} \right) $
Hence, we have proved that the area of a rhombus is equal to half the rectangle contained by its diagonals.

Note: It is important that you know all the formulas related to different quadrilaterals and even some of the important polygons. Also, it is very important that you don’t get confused between the areas of a trapezium and a rhombus and commit mistakes. It is also an important thing that you interpret the question correctly, as if you can’t understand the question correctly you cannot solve it as well.