
Prove that the bisectors of two adjacent supplementary angles include a right angle.
Answer
431.2k+ views
Hint: To prove that the bisectors of two adjacent supplementary angles include a right angle we draw the supplementary angles and also construct the angle bisectors of both the angles. Then use the property of angle bisectors to get the values of these angles. Now, we realize that all the angles lie on the same line so we use the property that the sum of all angles will be equal to
Complete step-by-step answer:
To prove that the bisectors of two adjacent supplementary angles include a right angle we draw the supplementary angles and also construct the angle bisectors of both the angles.
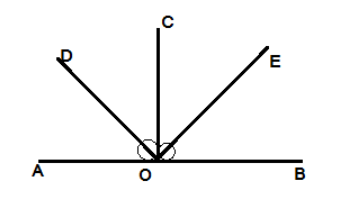
In the above diagram
In the above diagram we construct OD and OE.
OD is the angle bisector of angle
As we know that the angle bisector bisects the angle into two equal parts.
So,
AB is a straight line and the sum of all angles lying on a straight line is
So, we can first equate the sum of the two supplementary angles to
Put the values from eq. (i)
Hence proved
The bisectors of two adjacent supplementary angles include a right angle.
Note: In the given problem the property of straight line is used. Students must remember while drawing the supplementary angles that the sum of the measures of two angles is
Complete step-by-step answer:
To prove that the bisectors of two adjacent supplementary angles include a right angle we draw the supplementary angles and also construct the angle bisectors of both the angles.

In the above diagram
In the above diagram we construct OD and OE.
OD is the angle bisector of angle
As we know that the angle bisector bisects the angle into two equal parts.
So,
AB is a straight line and the sum of all angles lying on a straight line is
So, we can first equate the sum of the two supplementary angles to
Put the values from eq. (i)
Hence proved
The bisectors of two adjacent supplementary angles include a right angle.
Note: In the given problem the property of straight line is used. Students must remember while drawing the supplementary angles that the sum of the measures of two angles is
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




