Question

Prove that the external bisector of an angle of triangle divides the opposite side externally in the ratio to the sides containing the angle.

Answer 1

Hint: The given question is a named theorem called the angle bisector theorem. The angle bisector theorem is defined for internal angles and also external angles.
Here, we are asked to prove the external angle bisector theorem.
Let us consider $\Delta ABC$ where $AD$ is the external bisector. The angle bisector is nothing but a line or line segment which divides the angle into two equal parts.
Now, we need to prove that the external bisector of an angle of a triangle divides the opposite side externally in the ratio to the sides containing the angle.

Complete step-by-step solution:

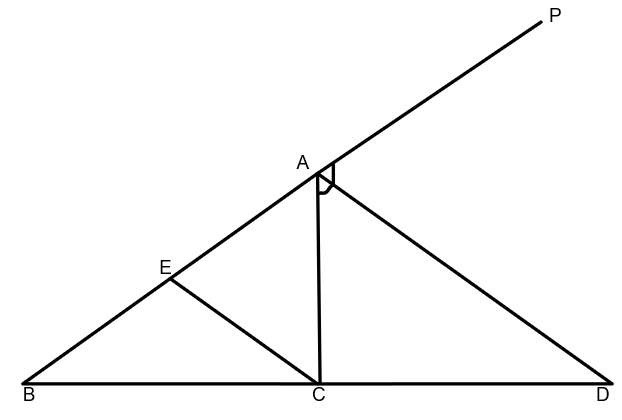
From the given information, let $AD$ be the external bisector of $\Delta BAC$ which intersects $BC$ produced at $D$ .
To verify:
$\dfrac{{BD}}{{DC}} = \dfrac{{AB}}{{AC}}$
Now, draw $CE\parallel DA$ meeting $AB$ at $E$ .
Since $CE\parallel DA$ and $AC$ is a transversal, we get $\angle ECA = \angle CAD$..\[\left( 1 \right)\]
Where, $\angle ECA$ and $\angle CAD$ are alternate angles again, $CE$ is parallel to $DA$ and $BP$ is a transversal, so
$\angle CEA = \angle DAP$…..\[\left( 2 \right)\]
Where, $\angle CEA$ and $\angle DAP$ are corresponding angles,
Since $AD$ is the bisector of $\angle CAP$ ,
$\angle CAD = \angle DAP$ … \[\left( 3 \right)\]
We know that, the sides opposite to equal angles are equal, by using this statement and also from\[\left( 1 \right)\],\[\left( 2 \right)\] and \[\left( 3 \right)\]
We have
$\angle CEA = \angle ECA$
Also, $EC\parallel AD$ in $\angle BDA$, so we have
$\dfrac{{BD}}{{DC}} = \dfrac{{BA}}{{AE}}$ (By Thales theorem)
And we know, $\angle CEA = \angle ECA \Rightarrow AE=AC$
Substituting $AE = AC$ in the above equation, we get
$\dfrac{{BD}}{{DC}} = \dfrac{{BA}}{{AC}}$ which is the required result.
Hence the theorem is proved.

Note: Thales theorem is introduced by Thales which is also called basic proportionality theorem; and this theorem proved that the ratio of any two corresponding sides is always same for any two equiangular triangles.
If an internal angle bisector theorem is asked to prove, follow the same procedure as we did for the external angle bisector theorem.