Question

Prove that the medians of an equilateral triangle are equal.

Answer 1

Hint: Draw meridians AE , BD and CF and use their properties to find congruence in the triangles $\vartriangle AEC,\vartriangle ABD,\vartriangle AFC$ and use CPCT to prove the meridians of an equilateral triangle are equal.

Complete step-by-step answer:

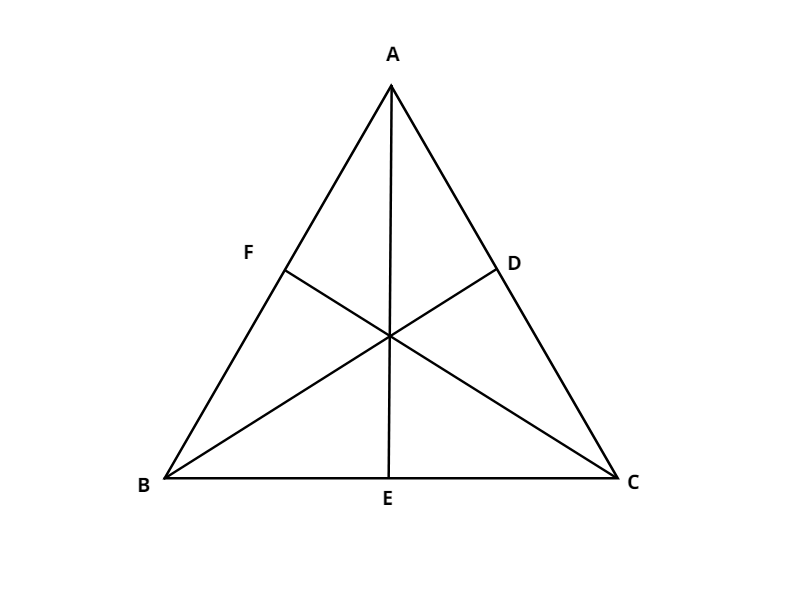
Let ABC be the equilateral triangle.
Then we have,
Angle A= $60^\circ $
Angle B= $60^\circ $
Angle C= $60^\circ $and,
AB=BC=AC
Let AE, BD and CF be the medians.
A meridian divides a side into two equal parts.
$ \Rightarrow $AB=BC=AC
$ \Rightarrow $AF+BF=BE+CE=AD+CD
$ \Rightarrow $2AF=2BE=2AD ( since the parts are equal )
$ \Rightarrow $AF=BE=AD
Therefore ,
AF=BF=BE=CE=AD=CD (1)
In $\vartriangle AEC$and $\vartriangle ABD$ we have,
AC=AB ( from the property of equilateral triangle )
$\angle C = \angle A$
EC=AD ( from equation 1 )
By SAS congruence criterion we get,
$\vartriangle AEC \cong \vartriangle ABD$
By Corresponding Parts of Congruent Triangle rule we get,
AE=BD (2)
Similarly,
$\vartriangle ABD \cong \vartriangle AFC$ ( By SAS congruence criterion )
$ \Rightarrow \vartriangle ABD \cong \vartriangle AFC$ ( From above )
Then,
BD=CF (3)
By equating equation 2 and equation 3 we get,
AE=CF=BD
Hence, proved that medians of an equilateral triangle are equal .

Note:In such types of questions , the triangle congruence rules must be remembered and used to get to the required answer . Also the properties of meridian should be recalled . Remember while using SAS congruence rule , the Angle should include the included angle of both sides .