Question

What is the radius of the circle with area 9?

Answer 1

Hint: In this problem, we have to find the radius of the circle, where we have been provided its area. We know that the formula for the area of the circle is \[\pi {{r}^{2}}\], where r is the radius. We are already given the area value, we can equate the area formula and the given area value to find the radius of the given circle.

Complete step by step solution:
Here we have to find the radius of the circle whose given area is 9.
We know that the area of the circle formula is,
Area of the circle = \[\pi {{r}^{2}}\].
We can now equate the given area of the circle value and the above formula for the area of the circle, we get
\[\Rightarrow \pi {{r}^{2}}=9\]
We can now divide \[\pi \] on both sides, we get
\[\Rightarrow {{r}^{2}}=\dfrac{9}{\pi }\]
We can now take square root on both sides, we get
\[\Rightarrow r=\dfrac{3}{\sqrt{\pi }}\]
We can now simplify the above step, we get
\[\Rightarrow r=1.69\]
Therefore, the radius of the circle is 1.69 whose area given is 9.

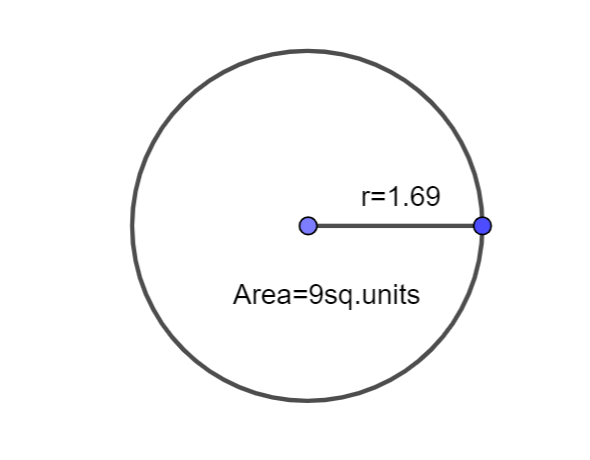
Note: Students make mistakes while writing the formula part for the area of the circle. We should know that the formula for the area of the circle is \[\pi {{r}^{2}}\]. We should always remember the value of \[\pi \] as we have to substitute to get the exact value for the required radius of the given circle. We will get two values in both positive and negative while taking the square root, where we have to take the positive value as radius must be in positive value.