Question

What is the radius of the incircle of a triangle whose sides are 5, 12 and 13 units?

Answer 1

Hint: In the above question, we are given a triangle with sides 5, 12 and 13. Inside the triangle, there is a circle touching all three sides of the triangle called an incircle. We have to find the radius of that incircle. In order to approach that, we can use the property of a circle that the tangents drawn from an exterior point to a circle are equal. After finding all three sides in terms of radius r, we can then solve for r

Complete step by step answer:
The diagram of the triangle and the incircle is shown below:

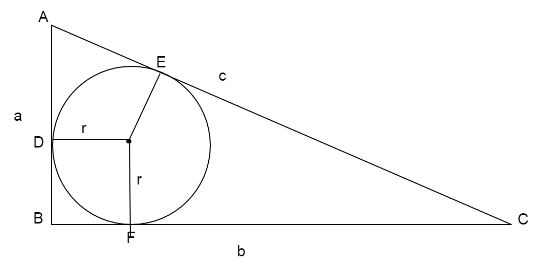
Here $a, b, c$ are $5, 12, 13$ respectively, and $r$ is unknown. Given that, ABC is a triangle with sides a, b and c as 5, 12 and 13 respectively. Circle EFD is the incircle of triangle ABC with radius r. We have to find the value of $r$. Now, we know that the two tangents that are drawn from an exterior point to a circle are equal.
Therefore, from the figure
\[ \Rightarrow BF = BD = r\]
Similarly,
\[ \Rightarrow AD = AE = a - r\]
Again,
\[ \Rightarrow CE = CF = b - r\]
Now, consider the side AC
\[ \Rightarrow AC = AE + CE\]

Putting the values of AC,AE and CE, we get
\[ \Rightarrow AC = c = a - r + b - r\]
Or we can write is as,
\[ \Rightarrow c = a + b - 2r\]
Adding \[2r\] both sides, we get
\[ \Rightarrow c + 2r = a + b\]
Subtracting c from both sides, gives us
\[ \Rightarrow 2r = a + b - c\]
Dividing both sides by 2, we get
\[ \Rightarrow r = \dfrac{{a + b - c}}{2}\]

Now, putting the values of a, b and c as 5, 12 and 13 respectively, we can write the above equation as
\[ \Rightarrow r = \dfrac{{5 + 12 - 13}}{2}\]
Solving the RHS, we get
\[ \Rightarrow r = \dfrac{{17 - 13}}{2}\]
\[ \Rightarrow r = \dfrac{4}{2}\]
Therefore,
\[ \therefore r = 2\]
That is the required radius of the incircle as \[r = 2\] .

Therefore the radius of the incircle of a triangle whose sides are 5, 12 and 13 units is 2 units.

Note: In the given triangle ABC, the sides are 5, 12 and 13 units.
Here, using the Pythagorean Theorem, we can see that
\[ \Rightarrow {5^2} + {12^2} = {13^2}\]
as
\[ \Rightarrow 25 + 144 = 169\]
Hence,
\[ \Rightarrow A{B^2} + A{C^2} = A{C^2}\]
Therefore the above triangle ABC is a right angled triangle.