Question

Rain is falling vertically with a speed of 30 m/s. A woman rides a bicycle with a speed of 10m/s in the north to south direction. What is the direction in which she should hold her umbrella then?

Answer 1

Hint: This is a question of vector addition and parallelogram law of vector addition can be applied to it. By using the properties of the right angle triangle we need to find the angle (tan$\theta$) that the resultant (from parallelogram law) makes with the vertical (rain direction).

Formula used:
The angle is obtained by the relation:
$\tan \theta =\dfrac{r_2}{r_1}$

Where $r_1$ is the magnitude of the vector along the horizontal axis and $r_1$ is the magnitude of the vector along the vertical axis.

Complete step by step answer:
A rough diagram of rain and cycle motion as vectors can be drawn as:

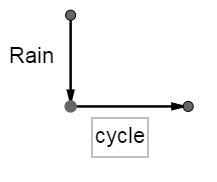
Thus, if we see the rain vector in a reversed position, we can use parallelogram law of vector addition.

Parallelogram law:
When two vectors have a common tail, their resultant is obtained by parallelogram law. If two vectors are such that the tail of one coincides with the head of another, we can reverse the sign of one of the vectors like in our case; we have to put a vector with a minus sign for the case of rain velocity.

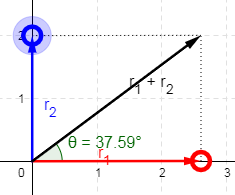
Thus, to find out the value of $\theta$, we see the right angled triangle that the two vectors make, and we write:
$\tan \theta =\dfrac{r_2}{r_1}$

But, we want to find the angle that the umbrella has to make with the vertical axis, so we use another triangle that has $r_1$ perpendicular and $r_2$ the base of the right angled triangle.

In our case, by using this example, we can write:

$\tan \theta =\dfrac{cycle}{rain}$

Here, rain is for velocity of rain and cycle is for the velocity of the cycle.
Without considering the direction of rainfall and bicyclist as only magnitude of the vector is required, we may write:
$\tan \theta =\dfrac{10}{30}$
$\theta = \arctan(\dfrac{1}{3})$
$\theta = 18.435^{\circ}$approximately.
The angle that the umbrella should make with the vertical axis is approximately $186^{\circ}$.

Note:
Since we were asked to find the direction in which the umbrella is to be held, we had to find the $\theta$ that the umbrella should make with the rain direction. The angle of the concerned right angled triangle should be noted carefully. We are concerned with the tan of the angle that the resultant (obtained from parallelogram) law makes with the vertical axis like angle between $r_1+r_2$ and $r_2$ in the figure.