
Represent \[\sqrt 3 \] on the real line.
Answer
563.4k+ views
Hint: Here we will use the Pythagoras Theorem for the representation of irrational numbers on the number line which states that:
It \[{\text{ABC}}\] is a right-angled triangle having \[{\text{AB}}\] as the perpendicular, \[{\text{BC}}\] as the base, and \[{\text{AC}}\] as the hypotenuses as shown in the below diagram:
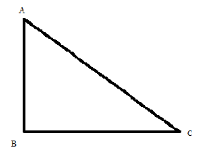
Then, the formula for finding the hypotenuses is as below:
\[{\text{AC = }}\sqrt {{{\left( {{\text{AB}}} \right)}^2} + {{\left( {{\text{BC}}} \right)}^2}} \]
Complete step-by-step answer:
Step 1: First of all, we will draw a number line as shown below where \[{\text{O}}\] are the center of the line and the right side we will write all positive integers will come, and on the left side, we will write all negative integers.
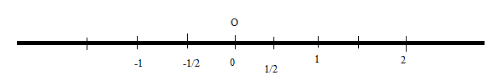
Step 2: Now, for representing \[\sqrt 3 \] on the real number line, we make a right-angled triangle from the point \[{\text{O}}\] as shown below:
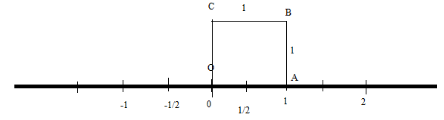
Here, \[{\text{A}}\] is the point that denotes
\[1\] the number line, so \[{\text{OA = 1}}\]. Now we will draw a perpendicular from the point
\[{\text{A}}\] to a point \[{\text{B}}\] , so that \[{\text{AB = 1}}\] because it is the same distance in the number as \[{\text{OA = 1}}\].
Step 3: Now, by joining the points \[{\text{B}}\] and \[{\text{C}}\], we get a right-angled triangle as shown below:
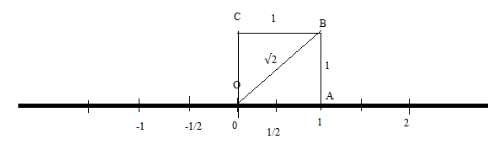
By using Pythagoras theorem in the triangle \[{\text{OAB}}\]:
\[{\text{OB = }}\sqrt {{{\left( {{\text{OA}}} \right)}^2} + {{\left( {{\text{AB}}} \right)}^2}} \]
By substituting the values of \[{\text{OA = 1}}\]and \[{\text{AB = 1}}\]in the above expression \[{\text{OB = }}\sqrt {{{\left( {{\text{OA}}} \right)}^2} + {{\left( {{\text{AB}}} \right)}^2}} \] , we get:
\[ \Rightarrow {\text{OB = }}\sqrt {{{\left( 1 \right)}^2} + {{\left( 1 \right)}^2}} \]
By opening the brackets and adding inside the root, we get:
\[ \Rightarrow {\text{OB = }}\sqrt 2 \]
Step 4: Now, by again drawing a perpendicular from a point \[{\text{B}}\] to \[{\text{E}}\] of length \[{\text{1 unit}}\] as shown below:
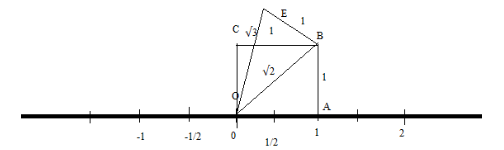
By applying Pythagoras theorem in the right-angled triangle \[{\text{OEB}}\] with \[{\text{OB = }}\sqrt 2 \] and \[{\text{BE = 1}}\], we get:
\[ \Rightarrow {\text{OE = }}\sqrt {{{\left( {{\text{OB}}} \right)}^2} + {{\left( {{\text{BE}}} \right)}^2}} \]
By substituting the values of \[{\text{OB = }}\sqrt 2 \]and \[{\text{BE = 1}}\] in the above expression \[ \Rightarrow {\text{OE = }}\sqrt {{{\left( {{\text{OB}}} \right)}^2} + {{\left( {{\text{BE}}} \right)}^2}} \] , we get:
\[ \Rightarrow {\text{OE = }}\sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( 1 \right)}^2}} \]
By opening the brackets inside the root, we get:
\[ \Rightarrow {\text{OE = }}\sqrt {2 + 1} \]
By doing the addition of the brackets inside the root, we get:
\[ \Rightarrow {\text{OE = }}\sqrt 3 \]
Step 5: Now, we will draw an arc from the center point \[{\text{O}}\] by taking the radius \[{\text{OE}}\] which will cuts the number line into the right side of the center at the point \[{\text{M}}\] which will represent \[\sqrt 3 \] the number line.
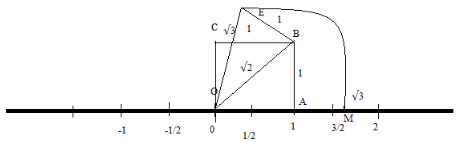
The point $\sqrt3 $ on the number line is
Note: Students need to take care while drawing the diagrams or by taking numbers on the number line. Sometimes, they take positive integers on the left side and negative integers on the right-hand side from the Centre of the number line which can lead to the incorrect answer.
It \[{\text{ABC}}\] is a right-angled triangle having \[{\text{AB}}\] as the perpendicular, \[{\text{BC}}\] as the base, and \[{\text{AC}}\] as the hypotenuses as shown in the below diagram:

Then, the formula for finding the hypotenuses is as below:
\[{\text{AC = }}\sqrt {{{\left( {{\text{AB}}} \right)}^2} + {{\left( {{\text{BC}}} \right)}^2}} \]
Complete step-by-step answer:
Step 1: First of all, we will draw a number line as shown below where \[{\text{O}}\] are the center of the line and the right side we will write all positive integers will come, and on the left side, we will write all negative integers.
Step 2: Now, for representing \[\sqrt 3 \] on the real number line, we make a right-angled triangle from the point \[{\text{O}}\] as shown below:

Here, \[{\text{A}}\] is the point that denotes
\[1\] the number line, so \[{\text{OA = 1}}\]. Now we will draw a perpendicular from the point
\[{\text{A}}\] to a point \[{\text{B}}\] , so that \[{\text{AB = 1}}\] because it is the same distance in the number as \[{\text{OA = 1}}\].
Step 3: Now, by joining the points \[{\text{B}}\] and \[{\text{C}}\], we get a right-angled triangle as shown below:

By using Pythagoras theorem in the triangle \[{\text{OAB}}\]:
\[{\text{OB = }}\sqrt {{{\left( {{\text{OA}}} \right)}^2} + {{\left( {{\text{AB}}} \right)}^2}} \]
By substituting the values of \[{\text{OA = 1}}\]and \[{\text{AB = 1}}\]in the above expression \[{\text{OB = }}\sqrt {{{\left( {{\text{OA}}} \right)}^2} + {{\left( {{\text{AB}}} \right)}^2}} \] , we get:
\[ \Rightarrow {\text{OB = }}\sqrt {{{\left( 1 \right)}^2} + {{\left( 1 \right)}^2}} \]
By opening the brackets and adding inside the root, we get:
\[ \Rightarrow {\text{OB = }}\sqrt 2 \]
Step 4: Now, by again drawing a perpendicular from a point \[{\text{B}}\] to \[{\text{E}}\] of length \[{\text{1 unit}}\] as shown below:

By applying Pythagoras theorem in the right-angled triangle \[{\text{OEB}}\] with \[{\text{OB = }}\sqrt 2 \] and \[{\text{BE = 1}}\], we get:
\[ \Rightarrow {\text{OE = }}\sqrt {{{\left( {{\text{OB}}} \right)}^2} + {{\left( {{\text{BE}}} \right)}^2}} \]
By substituting the values of \[{\text{OB = }}\sqrt 2 \]and \[{\text{BE = 1}}\] in the above expression \[ \Rightarrow {\text{OE = }}\sqrt {{{\left( {{\text{OB}}} \right)}^2} + {{\left( {{\text{BE}}} \right)}^2}} \] , we get:
\[ \Rightarrow {\text{OE = }}\sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( 1 \right)}^2}} \]
By opening the brackets inside the root, we get:
\[ \Rightarrow {\text{OE = }}\sqrt {2 + 1} \]
By doing the addition of the brackets inside the root, we get:
\[ \Rightarrow {\text{OE = }}\sqrt 3 \]
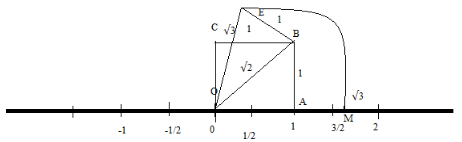
Step 5: Now, we will draw an arc from the center point \[{\text{O}}\] by taking the radius \[{\text{OE}}\] which will cuts the number line into the right side of the center at the point \[{\text{M}}\] which will represent \[\sqrt 3 \] the number line.

The point $\sqrt3 $ on the number line is

Note: Students need to take care while drawing the diagrams or by taking numbers on the number line. Sometimes, they take positive integers on the left side and negative integers on the right-hand side from the Centre of the number line which can lead to the incorrect answer.

Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

What is pollution? How many types of pollution? Define it




