Question

Rinku has built a cuboidal water tank in his house. The top of the water tank is covered with an iron lid. He wants to cover the inner surface of tank including the base with tiles of size $ 10\text{ cm}\times \text{8 cm} $ . If the dimensions of the water tank are $ 180\text{ cm}\times \text{120 cm}\times 60\text{ cm} $ and cost of tiles is Rs. 480 per dozen, then find the total amount required for tiles. \[\]

Answer 1

Hint: We find the area of the inner tank by removing the area for the top as $ {{A}_{c}}=l\times b+2\left( b\times h+h\times l \right) $ . We find the area of the 1 tile as $ {{A}_{t}}={{l}_{t}}\times {{b}_{t}} $ . We find number of tiles required as $ n=\dfrac{{{A}_{c}}}{{{A}_{t}}} $ . We find the cost 1 tiles and then the cost of 720 tiles. \[\]

Complete step by step answer:
We know that a cuboid is a three dimensional object with six rectangular faces joined by 8 vertices. It has three different types of sides called length, breadth and height denoted $ l, $ $ b $ and $ h $ . The total surface area is the sum of three type types of surfaces which is
\[TSA=2\left( l\times b+b\times h+h\times l \right)\]
We are given in the question that the dimensions of the cuboidal shaped water tank are $ 180\text{ cm}\times \text{120 cm}\times 60\text{ cm} $ . So we have length, breadth and height of the inner cuboid in order as;
\[l=180\text{ cm},b=120\text{ cm},h=60\text{ cm}\]

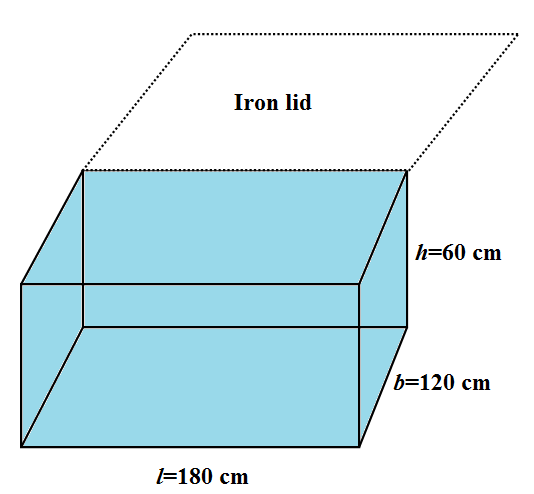
We are given that the top of the water tank is covered with an iron lid. Hence the tiles cannot be covered on the top. Hence the surface area on which Rinku can cover the tiles is total surface of the cuboidal tank excluding the area of top that that is
\[\begin{align}
  & {{A}_{c}}=l\times b+2\left( b\times h+h\times l \right) \\
 & \Rightarrow A=180\times 120+2\left( 1200\times 60+60\times 180 \right) \\
 & \Rightarrow A=21600+36000 \\
 & \Rightarrow A=576\text{ c}{{\text{m}}^{2}} \\
\end{align}\]
We are given that the tiles are size $ 10\text{ cm}\times \text{8 cm} $ . So area of 1 tile is
\[{{A}_{t}}=10\times 8=80\text{ c}{{\text{m}}^{2}}\]
So $ 80\text{ c}{{\text{m}}^{2}} $ of surface is covered by 1 tile. The total surface area of the inner cuboidal tank will be covered by
\[\dfrac{{{A}_{c}}}{{{A}_{t}}}=\dfrac{57600}{80}=720\]
We are given that 12 tiles cost 480 rupees, so 1 tile will cost $ \dfrac{480}{12}=40 $ rupees. So the total amount to cover the inner surface of the tank is the cost of 720 tiles that is
\[720\times 40=28800\text{ rupees}\]
Note:
We note that a dimension of the cuboid is always mentioned in the form $ l\times b\times h $. We have assumed $ l\times b\times h $ the dimensions of the inner cuboid, not the outer cuboid because there is the thickness in between them. We note that the area of the rectangle is $ l\times b $ . We have used the unitary method in direct variation to find the total amount because as the number of tiles increases the cost also increases. The volume of a cuboid will not change even if a surface is removed and remains the same as $ V=l\times b\times h $.