Question

Rohit focused the image of the candle flame on a white screen using a convex lens He noted down the position of the candle, screen and lens under:
\[\begin{align}
  & \text{Position of the candle= 26 cm} \\
 & \text{Position Of Convex Lens=50cm} \\
 & \text{Position Of The Screen=74cm} \\
\end{align}\]
a) What is the focal length of the convex lens
b) What will be the image formed if he shifts the candle towards the lens at a position of 38 cm
c) Draw the ray diagram to show the formation of image in case (ii) as said above

Answer 1

Hint: First draw the ray diagram for the given experiment conducted. The distances mentioned above are measured from a fixed point on the side of the convex lens where the candle is kept. To find the answer to the question asked, in the lens formula use the sign convention according to the ray diagram and not directly according to the given distances above.

Complete answer: To begin with let us first draw a rough ray diagram of the experiment conducted above.

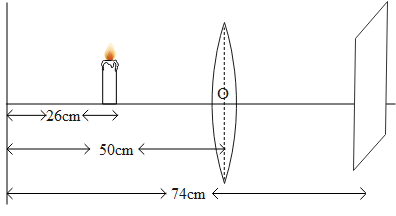
From the above diagram,
The object distance from the lens is i.e. u= 50-26 = - 24 cm
The distance of the image formed on the screen to the lens i.e. v= 74-50 = 24 cm
Using the lens formula let us find the focal length of the lens

$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$ where f is the focal length of the lens, v is the image distance and u is the object distance.
$\dfrac{1}{f}=\dfrac{1}{24}-\dfrac{1}{-24}$
$\dfrac{1}{f}=\dfrac{1}{24}+\dfrac{1}{24}=\dfrac{2}{24}=\dfrac{1}{12}$
$f=12cm$
Hence focal length of the lens is 12 cm.

Now let us find out where the image will be formed when the candle is positioned at 38 cm. When the candle is positioned at 38 cm. The distance between the lens and the candle is 50 – 28 = -12cm.
Hence using lens formula let us find the image distance
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$
$\begin{align}
  & \dfrac{1}{12}=\dfrac{1}{v}+\dfrac{1}{12} \\
 & \\
\end{align}$

$\dfrac{1}{12}-\dfrac{1}{12}=\dfrac{1}{v}=0$
$\dfrac{1}{v}$ is zero hence $v=\infty $
Hence the image will be formed at an infinite distance as compared to the size of the apparatus used in the experiment.
Now let us draw the ray diagram for the above condition.

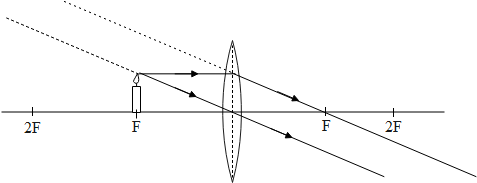
Note:
Only those distances are to be considered which are from the optical centre of the convex lens and not the position of the object with respect to some positioning system. While drawing the rays diagrams make sure they are symmetrical across the line passing through the optical centre. Otherwise there will be minute errors in comparison to the actual condition.