Question

How do you rotate the axes to transform the equation ${x^2} + xy = 3$ into a new equation with no $xy$ term and then find angle of rotation?

Answer 1

Hint: Transforming an equation means rotating the coordinate axes without shifting the origin by an angle $\theta $. The old coordinates can be represented by using new coordinates. Hence, substituting them in the equation given in the question will give us the new equation (after the rotation).
Let $(x,y)$ be old coordinates and $(x',y')$ be the new coordinates.
The relation between them can be given by the formula:
$x = x'\cos \theta - y'\sin \theta $ and $y = x'\sin \theta + y'\cos \theta $
Where $\theta $ is the angle of rotation of the coordinate axis.

Complete step-by-step answer:
Let’s draw a diagram to represent the rotation of axes.

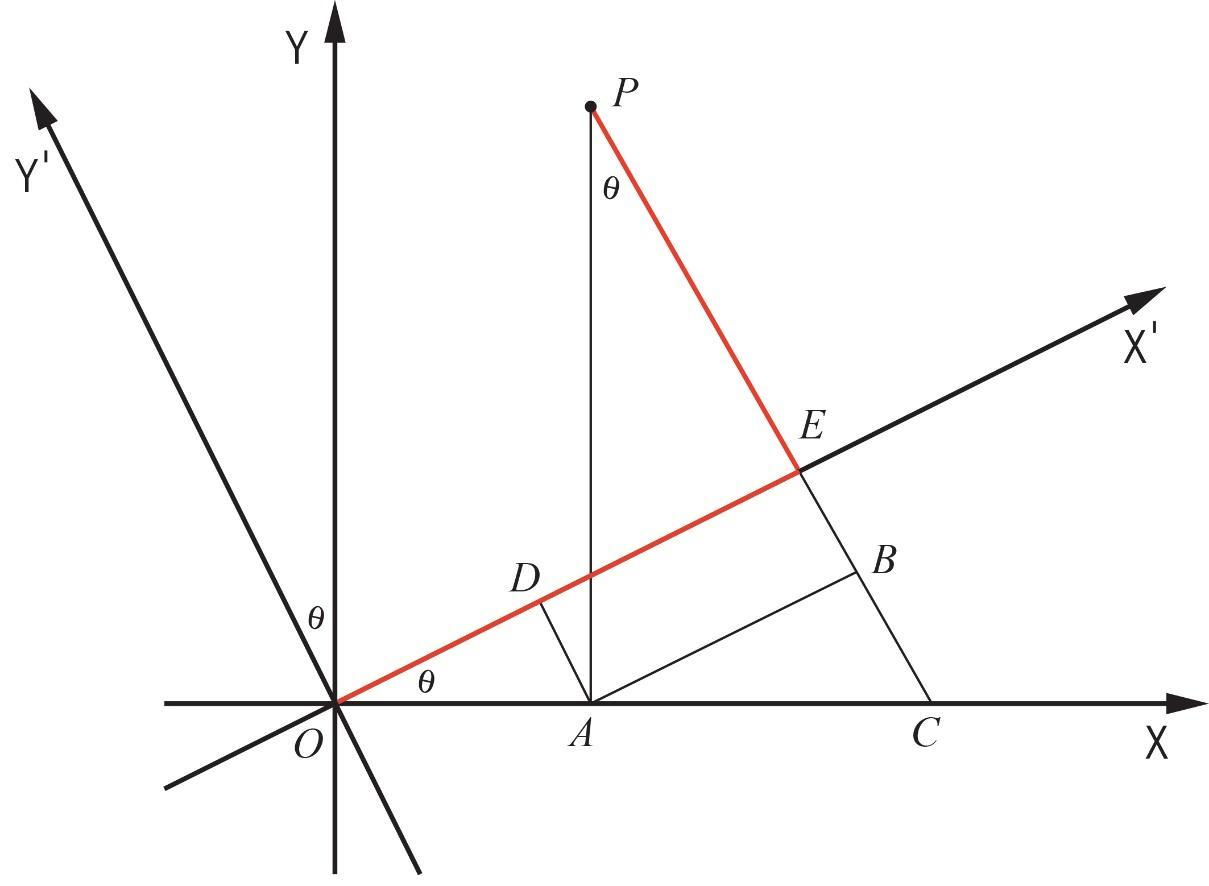
The old equation is ${x^2} + xy = 3$
When we substitute above mentioned new coordinates in place of old coordinates, we get:
${(x'\cos \theta - y'\sin \theta )^2} + (x'\cos \theta - y'\sin \theta )(x'\sin \theta + y'\cos \theta ) = 3$
By opening all the brackets, we get:
$(x{'^2}{\cos ^2}\theta + y{'^2}{\sin ^2}\theta - 2x'y'\sin \theta \cos \theta ) + (x{'^2}\cos \theta \sin \theta - y{'^2}\cos \theta \sin \theta + x'y'{\cos ^2}\theta - x'y'{\sin ^2}\theta ) = 3$
By taking out coefficients of same terms common we get;
$x{'^2}({\cos ^2}\theta + \cos \theta \sin \theta ) + y{'^2}({\sin ^2}\theta - \cos \theta \sin \theta ) + x'y'( - 2\cos \theta \sin \theta - {\sin ^2}\theta + {\cos ^2}\theta ) = 3$
In the question we are asked to eliminate the $xy$ term, so we have to make the coefficient of $xy$ term zero. By doing so we get;
$ - 2\cos \theta \sin \theta - {\sin ^2}\theta + {\cos ^2}\theta = 0$
$2\cos \theta \sin \theta = - {\sin ^2}\theta + {\cos ^2}\theta $
We know the basic trigonometric formulae:
$\sin 2\theta = 2\cos \theta \sin \theta $
\[\cos 2\theta = - {\sin ^2}\theta + {\cos ^2}\theta \]
By substituting the above formulae we get:
$\sin 2\theta = \cos 2\theta $
$\tan 2\theta = 1$
By using inverse trigonometric formula of tan, we get:
$2\theta = n\pi + \dfrac{\pi }{4}$
$\theta = \dfrac{{n\pi }}{2} + \dfrac{\pi }{8}$ where n can be any integer.
Hence, we can have more than one answer by taking different values of n.
Let’s take n value as zero, we get:
$x{'^2}({\cos ^2}22.5^\circ + \cos 22.5^\circ \sin 22.5^\circ ) + y{'^2}({\sin ^2}22.5^\circ - \cos 22.5^\circ \sin 22.5^\circ ) = 3$
We know that:
$\cos 22.5^\circ = 0.92$
$\sin 22.5^\circ = 0.38$
By substituting the corresponding values, we get:
$x{'^2}\left( {1.196} \right) + y{'^2}( - 0.2052) = 3$

Note: The above given equation is only one of the possible answers. There can be more than one solution by taking different values of n. We need to be careful while using the formulae and remembering the basic trigonometric formulae will always come in handy since they make the calculation a lot easier. When finding the new equation, there is a lot of calculation involved so one should be careful while doing the mathematics involved. The formula can be derived from basic congruence of the triangles.