Question

Ship A is sailing towards the north east with velocity $\vec v = 30\hat i + 50\hat jkm/hr$ where $\hat i$ points east $\hat j$ and north. Ship B is at a distance of 80 km east and 150 km north of ship A and is sailing towards west at 10 km/hr. A will be at minimum distance from B in
(A) $4.2$ hours
(B) $2.2$ hours
(C) $3.2$ hours
(D) $2.6$ hours

Answer 1

Hint: We know that the relation between time, velocity and displacement is given as
Time $ = \dfrac{{displacement}}{{velocity}}$
And the above expression is also applicable for relative motion like relative velocity, relative displacement etc. But time does not depend on frame of reference.

Complete step by step answer:

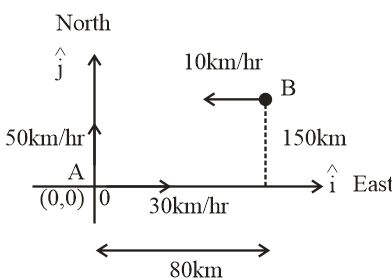
Given that initial positions of ship A & B is
${\vec r_A} = 0\hat i + 0\hat j$ …..(1)
${\vec r_B} = (80\hat i + 150\hat j)km$ ….(2)
So, the relative position of B with respect to A
${\vec r_{BA}} = (80\hat i + 150\hat j)km$ …..(3)
Also, given that the velocity of ship A & B is
${\vec v_A} = (30\hat i + 50\hat j)km/hr$
${\vec v_B} = - 10\hat ikm/hr$
So, relative velocity of B with respect to A is
${\vec v_{BA}} = - 10\hat i - (30\hat i + 50\hat j)$
$ = - 10\hat i - 30\hat i - 50\hat j$
${\vec v_{BA}} = - 40\hat i - 60\hat j$ …..(4)
And magnitude of ${\vec v_{AB}}$ is given as
\[|{\vec v_{BA}}| = \sqrt {{{(40)}^2} + {{(50)}^2}} \]
$\sqrt {1600 + 2500} $
$|{\vec v_{BA}}| = \sqrt {4100} $ …..(5)
We know that
Time t $ = \dfrac{{displacement(\vec r)}}{{velocity(\vec v)}}$
In relative motion
$t = \dfrac{{{{\vec r}_{BA}}}}{{{{\vec v}_{BA}}}}$
On multiplying ${\vec v_{BA}} \Rightarrow t = \dfrac{{{{\vec r}_{BA}} \cdot {{\vec v}_{BA}}}}{{{{\vec v}_{BA}} \cdot {{\vec v}_{BA}}}}$
$t = \dfrac{{{{\vec r}_{BA}} \cdot {{\vec v}_{BA}}}}{{|{{\vec v}_{BA}}{|^2}}}$
So, from equation 3, 4 & 5
$t = \dfrac{{(80\hat i + 150\hat j) \cdot ( - 40\hat i - 50\hat j)}}{{{{(\sqrt {4100} )}^2}}}$
$t = \dfrac{{[ - (80 \times 40)] + [ - (150 \times 50)]}}{{4100}}$
$t = \dfrac{{ - 3200 - 7500}}{{4100}} = \dfrac{{ - 10700}}{{4100}}$
Time never be –ve, hence
$t = \dfrac{{10700}}{{4100}} = \dfrac{{107}}{{41}} = 2.6$ hours
$t = 2.6$ hours

So, the correct answer is “Option D”.

Note:
Relative motion is a concept which makes numerical problems easy. We can apply the above formulae only when there is no acceleration given to particles. Time does not depend on frame of reference.