Question

Show that in an equilateral triangle, circumcentre, orthocenter and incenter overlap each other.

Answer 1

Hint: Draw a rough figure, the median will be perpendicular to the base. Thus draw medians from all vertices and find the centroid G. By using the property of equilateral triangle centroid is equidistant from the center.

Complete step-by-step answer:
Consider the figure that is drawn below. From the figure you can make out that ABC is the equilateral triangle.

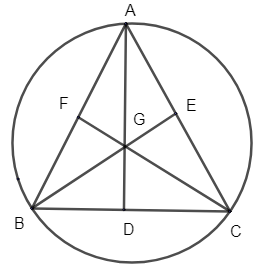
Now let us consider G as the centroid of equilateral \[\Delta ABC\].
Now from the figure, let us consider \[\Delta BEC\] and \[\Delta BCF\].
As the \[\Delta ABC\] is an equilateral triangle, all the angles are the same.
i.e. AB = BC = AC.
Similarly, in an equilateral triangle all the angles are the same.
i.e. \[\angle A=\angle B=\angle C={{60}^{\circ }}\]
Thus in \[\Delta BEC\] and \[\Delta BCF\].
\[\angle B=\angle C={{60}^{\circ }}\]
BC = BC, this side is common for both triangles.
BF = CE, these sides are equal.
Thus we can say that \[\Delta BEC\cong \Delta BCF\].
Thus \[\Delta BEC\] and \[\Delta BCF\] are similar. So we can say that the side BE will be equal to CF as triangles are similar.
\[\therefore BE=CF-(1)\]
Similarly, we can prove that \[\Delta CAF\cong \Delta CAD\] and from this we can make out that,
\[CF=AD-(2)\]
From (1) and (2) we can say that,
AD = BE = CF.
If we are considering the centroid of the triangle, the centroid theorem states that the centroid of the triangle is at \[\dfrac{2}{3}\] of the distance from the vertex to the midpoint of the side.
Thus, \[GA=\dfrac{2}{3}AD\].
Similarly, \[GB=\dfrac{2}{3}BE\] and \[GC=\dfrac{2}{3}CF\].
i.e. We can say that G is equidistant from the vertices.
Thus we can say that G is the circumcenter of \[\Delta ABC\].
Hence we have proved that in the equilateral triangle the centroid and the circumcenter of the triangle coincide.

Note: In the case of an equilateral triangle to find the centroid we can use the centroid theorem. If the coordinates of a triangle is given, the centroid of the triangle can be found by using a formula. The 3 vertices are \[A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right)\].
\[\therefore \] Centroid \[=\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\].