Question

Show that the function \[f:R \to R\]given by \[f(x) = {x^3}\;\]is injective

Answer 1

Hint: since we know the graph of the function hence we will draw the
graph of this function and then solve

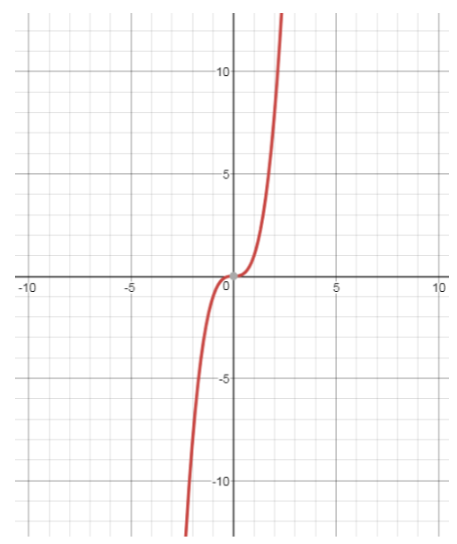
Now from the graph we can solve the question easily
Since we know that
A function is a one-to-one function if and only if each second element corresponds to one and only one first element. (each $x$ and $y$ value is used only once)
Now we use the horizontal line test to determine whether the function is one to one or not

The horizontal line test is
If ANY horizontal line intersects your original function in ONLY ONE location, your function will be a one-to-one function and its inverse will also be a function.

Now if we draw a horizontal line in this graph it will intersect the graph only at once place hence it is one-to-one function

Which could also be proved as
Let assume that \[x,y \in R\;\]such that
 \[
  f(x) = f(y) \\
   \Rightarrow {x^3} = {y^3} \\
   \Rightarrow x = y \\
\]
Hence we again prove that the function is one to one function
Now a function is injective if it is a ONE-TO-ONE
Hence we have that this function is ONE-TO-ONE hence this function is an injective function.

Note: While testing any function for injective function or one-to-one function or bijective function or any other we should draw their graph if we know them and then solve them then it is easy.

.