Question

Show that the torque on an electric dipole placed in a uniform electric field is $\overrightarrow \tau = \overrightarrow {\text{P}} \times \overrightarrow {\text{E}} $.

Answer 1

Hint: Here, we will proceed by writing down the forces experienced by the charges in the electric dipole placed in a uniform electric field. Then, we will obtain the expression corresponding to the torque experienced by these charges.
Formulas Used: $\tau = {\text{Fr}}\sin \theta $, ${\text{p}} = {\text{qd}}$.

Complete Step-by-Step solution:

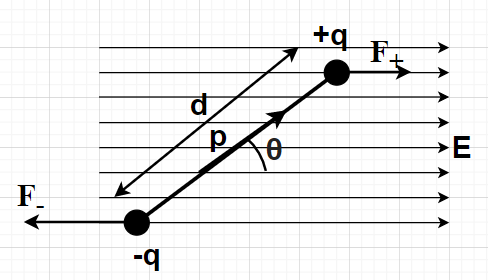
To show: $\overrightarrow \tau = \overrightarrow {\text{P}} \times \overrightarrow {\text{E}} $
The force measure which causes an object to rotate about an axis is called the torque. Torque is a quantity of vectors, and its direction depends on the axis direction of force. The magnitude of the torque vector can be written as
$\tau = {\text{Fr}}\sin \theta $ where F denotes the force, r denotes the length (or radius) of the moment arm and $\theta $ denotes the angle between the moment arm and the force.
A pair of electric charges with an equal magnitude but opposite charges separated by a distance is known as an electric dipole. The electric dipole moment is defined as the product of the magnitude of either charge and the distance between these charges. The electric dipole moment is a vector quantity having a defined direction from the negative charge to the positive charge.
The magnitude of the electric dipole moment p is given by
${\text{p}} = {\text{qd}}$ where q denotes the magnitude of either charge and d denotes the distance between the two charges.
Consider an electric dipole with charges +q and –q forming a dipole since they are separated by distance d. Let it be placed in a uniform electric field of strength E such that the axis of the dipole forms an angle $\theta $ with the electric field.
The forces on these charges (+q and –q) when placed in the electric field having E as the electric field intensity are given by
${{\text{F}}_ + }$ = +qE
${{\text{F}}_ - }$ = -qE
Since, $\theta $ is the angle between the moment arm and the force. So, the sine component of this angle will be perpendicular to the moment arm and the cosine component of this angle will be along the moment arm.
The components of the forces exerted on the charges perpendicular to the dipole are given by
${{\text{F}}_1} = {\text{qE}}\sin \theta $
${{\text{F}}_2} = {\text{qE}}\sin \theta $
Since the magnitudes of the forces are equal. These charges are separated by a distance d, the torque on the dipole is given by:
Torque = Force $ \times $ distance by which the charges are separated
$
  \tau = \left( {{\text{qE}}\sin \theta } \right){\text{d}} \\
   \Rightarrow \tau = {\text{qdE}}\sin \theta \\
 $
Since dipole moment is given by p = qd
$ \Rightarrow \tau = {\text{pE}}\sin \theta {\text{ }} \to {\text{(1)}}$
Cross product of any two vectors $\overrightarrow a $ and $\overrightarrow b $ is given by
$\overrightarrow a \times \overrightarrow b = ab\sin \theta $ where $\theta $ denotes the angle between these vectors (i.e., $\overrightarrow a $ and $\overrightarrow b $), a and b are the magnitudes of $\overrightarrow a $ and $\overrightarrow b $ respectively.
Using the formula $\overrightarrow a \times \overrightarrow b = ab\sin \theta $, equation (1) becomes
$ \Rightarrow \tau = \overrightarrow {\text{p}} \times \overrightarrow {\text{E}} $
The above equation is the required equation which needed to be proved.

Note- The direction of the dipole moment is from the positive to the negative charge. Clearly, from the equation $\overrightarrow \tau = \overrightarrow {\text{P}} \times \overrightarrow {\text{E}} $, we can see that the torque is the cross product of the dipole moment and electric field. Notice that the torque is in the clockwise direction (hence negative) if the direction of the Electric Field is positive.