Question

How many sides do a polygon have whose sum of the interior angles is \[1980^\circ \]?
A) 10
B) 13
C) 11
D) None of the above

Answer 1

Hint: A polygon is a closed figure. It can have both regular and irregular sides. There is a formula that can be used to calculate the sum of interior angles using the sides of the polygon. So, in this case, the sum of interior angles is given, and we have to reverse the calculation to get the sides of the polygon.

Complete step by step answer:
The sum of interior angles of a polygon formula is based on the sum of interior angles of a triangle, which is \[180^\circ \]. So, we know that,
\[S = (n - 2) \times 180^\circ \]
Where n is the number of sides of the polygon and S is the sum of interior angles. Now, by putting the value of S as \[1980^\circ \] , we can derive the number of sides.
\[ \Rightarrow 1980^\circ = (n - 2) \times 180^\circ \]
By taking \[180^\circ \] on the other side, we get
\[ \Rightarrow \dfrac{{1980^\circ }}{{180^\circ }} = (n - 2)\]
\[ \Rightarrow 11 = (n - 2)\]
And finally, by taking 2 on the other side
\[ \Rightarrow 11 + 2 = n\]
\[ \Rightarrow n = 13\]
Hence, the number of sides in a polygon, having the sum of interior angles \[1980^\circ \], is 13.

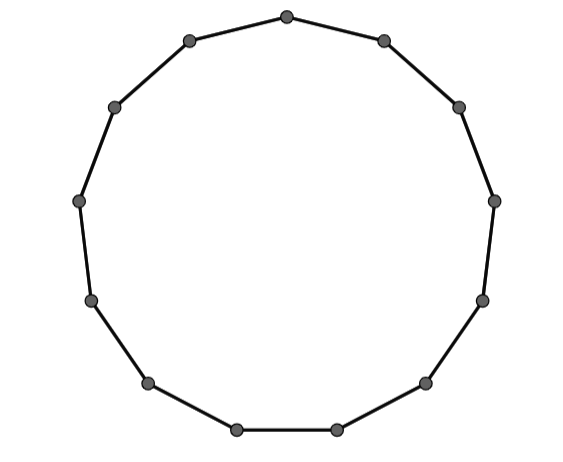
So, the correct answer is “Option B”.

Note:
Remember that we reversed the formula because the sum of interior angles was given. However, if the sides are specified in the question, we will put the value in n's place and calculate the total of internal angles. Also, there is a huge difference between the sum of interior angles and the sum of exterior angles, so don’t get confused between the two.