Question

Sketch the graph for \[y = {\sin ^{ - 1}}\left( {\sin x} \right)\]

Answer 1

Hint: In this question to draw the graph for \[y = {\sin ^{ - 1}}\left( {\sin x} \right)\] firstly find out the differentiation of the given function, then break the differential into intervals after that find out the second differential and break it in intervals and check concavity and you can make the graph of the given function.

Complete answer:
Trigonometry is a combination of the Greek word trigon and metron. Here, trigon refers to figures with three angles, and metron refers to the measurement, hence the definition of trigonometry is triangle measurement.
We know that the meaning of \[dx\] is the increment in \[x\] and it may be positive or negative. Similarly, \[dy\] means the increment in the value of \[y\]
If there is an increment in the value of \[x\] and \[y\] in the same direction either both positive or both negative then the value of \[\dfrac{{dy}}{{dx}}\] is always positive. On the other hand, if the increment in \[x\] and \[y\] are of positive direction that is one positive and other negative then the value of \[\dfrac{{dy}}{{dx}}\] will be negative.
Now according to the question:
We have to sketch the graph for \[y = {\sin ^{ - 1}}\left( {\sin x} \right)\] hence:
\[ \Rightarrow y = {\sin ^{ - 1}}\left( {\sin x} \right)\]
We will find out the differential of \[y\] :
\[ \Rightarrow y' = \dfrac{d}{{dx}}{\sin ^{ - 1}}\left( {\sin x} \right)\]
\[ \Rightarrow y' = \dfrac{1}{{\sqrt {1 - {{\sin }^2}x} }}\dfrac{d}{{dx}}\left( {\sin x} \right)\]
\[ \Rightarrow y' = \dfrac{{\cos x}}{{\sqrt {1 - {{\sin }^2}x} }}\]
As we know that \[1 - {\sin ^2}x = {\cos ^2}x\]
\[ \Rightarrow y' = \dfrac{{\cos x}}{{\sqrt {{{\cos }^2}x} }}\]
\[ \Rightarrow y' = \dfrac{{\cos x}}{{\left| {\cos x} \right|}}\]
Now break \[y'\] into intervals and simplify \[\left| {\cos x} \right|\]
$ \Rightarrow y' = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{\cos x}}{{\cos x}} = 1}&{ > 0}&{0 \leqslant x < \dfrac{\pi }{2}} \\ {\dfrac{{cosx}}{{ - \cos x}} = - 1}&{ < 0}&{\dfrac{\pi }{2} < x < \dfrac{{3\pi }}{2}} \\ {\dfrac{{\cos x}}{{\cos x}} = 1}&{ > 0}&{\dfrac{{3\pi }}{2} < x \leqslant 2\pi } \end{array}} \right.$
Now we will again find out differentiation of \[y'\] :
\[ \Rightarrow y'' = 0\]
Now break \[y''\] into intervals:
$ \Rightarrow y' = \left\{ {\begin{array}{*{20}{c}} 0&{0 \leqslant x < \dfrac{\pi }{2}} \\ 0&{\dfrac{\pi }{2} < x < \dfrac{{3\pi }}{2}} \\ 0&{\dfrac{{3\pi }}{2} < x \leqslant 2\pi } \end{array}} \right.$
Here the concavity is neither increasing nor decreasing hence there will only be a straight line:
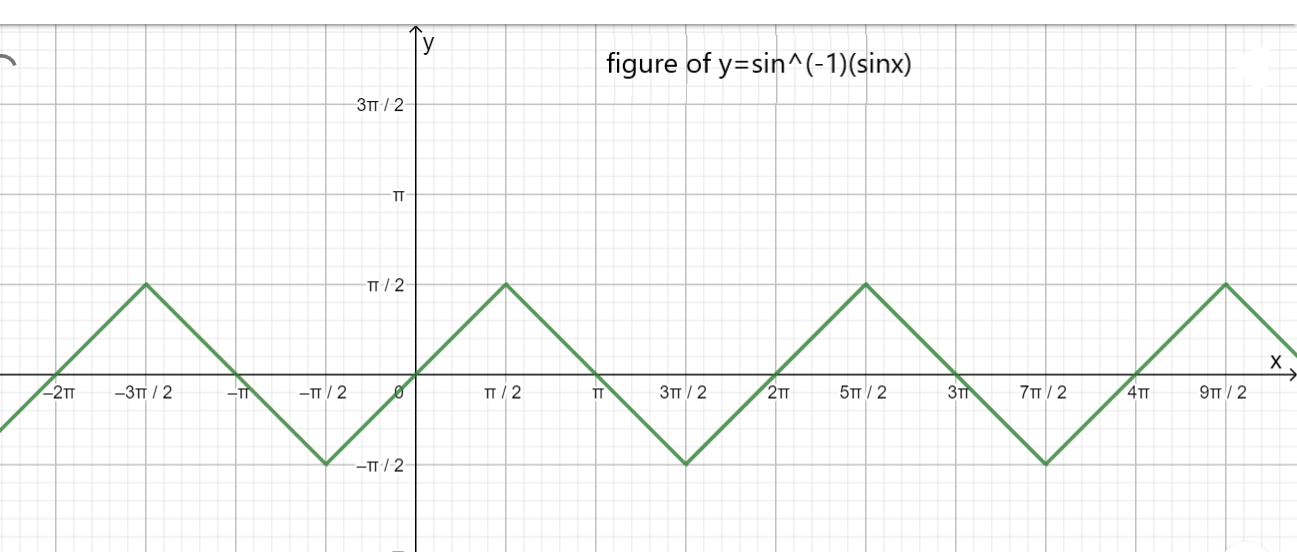
Now find out these points of the given function that is \[y = {\sin ^{ - 1}}\left( {\sin x} \right)\] hence:
\[ \Rightarrow y = {\sin ^{ - 1}}\left( {\sin 0} \right) = 0\]
\[ \Rightarrow y = {\sin ^{ - 1}}\left( {\sin \dfrac{\pi }{2}} \right) = \dfrac{\pi }{2}\]
\[ \Rightarrow y = {\sin ^{ - 1}}\left( {\sin \dfrac{{3\pi }}{2}} \right) = - \dfrac{\pi }{2}\]
\[ \Rightarrow y = {\sin ^{ - 1}}\left( {\sin 2\pi } \right) = 0\]
Now draw the graph from \[0\] to \[2\pi \]:

Note:
The word sine is derived from the Latin word sinus, which means 'bay' or 'fold.' This, in turn, is either derived from a bowstring-related phrase. Any trigonometric function of angle \[{\theta ^ \circ }\] is equal to the same trigonometric function of any angle \[n \times {360^ \circ } + \theta \] , where \[n\] is any integer.