Question

What is the smallest angle of rotational symmetry that a regular hexagon has?

Answer 1

Hint: In this problem, we have to find the smallest angle of rotational symmetry that a regular hexagon has. We should first know that a figure has rotational symmetry if it can be rotated by an angle between \[{{0}^{\circ }}\]and \[{{360}^{\circ }}\] so that the image coincides with the preimage. Here we can find the angle of rotations of a regular hexagon and we can find the smallest one among them.

Complete step by step solution:
Here we have to find the smallest angle of the regular hexagon’s rotational symmetry.
We should know that a regular hexagon has 6 sides. We should first know that a figure has rotational symmetry if it can be rotated by an angle between \[{{0}^{\circ }}\]and \[{{360}^{\circ }}\] so that the image coincides with the preimage.
We know that a hexagon has three rotations, so we can write
\[\Rightarrow {{360}^{\circ }}\div 6=60\]
We also know that the angle of rotations of the hexagon are,
\[{{60}^{\circ }},{{120}^{\circ }},{{180}^{\circ }},{{240}^{\circ }},{{300}^{\circ }},{{360}^{\circ }}\]
Where, the smallest rotational angle is \[{{60}^{\circ }}\].

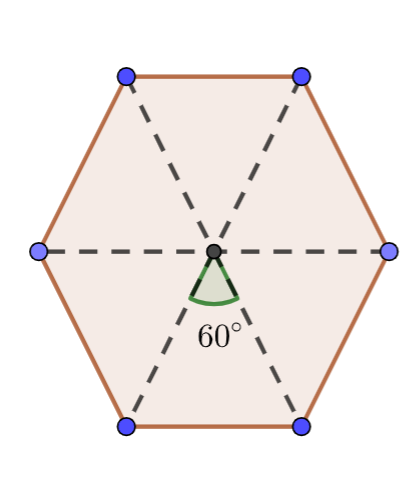
Therefore, the smallest angle of rotational symmetry that a regular hexagon has is \[{{60}^{\circ }}\].

Note: We should remember that the angle of rotational symmetry is the smallest angle for which the figure can be rotated to coincide with itself. The order symmetry is the number of times the figure coincides with itself as it rotates through \[{{360}^{\circ }}\]. We should also know that the order of rotational symmetry is 6.