
Answer
495.6k+ views
Hint: We had to only assume that the line PQ is mirror and then shade only those squares whose mirror image (i.e. image formed by the reflection of any shape from the mirror) is shaded.
Complete step-by-step answer:
Now as we know that the mirror image of any shape is the image formed when we reflect the image with the mirror.
And any line will be the line of symmetry if all the images on the opposite side of that line have its mirror image the same as that image if the mirror is the line itself.
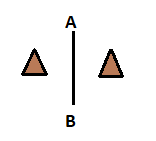
Like in the above figure AB will be the line of symmetry because both the triangles on the opposite side of the AB are mirror images of each other and they are identical.
Now as we know that we had to find the minimum number of squares that should be shaded. So, the line PQ became the line of symmetry.
So, PQ will be the line of symmetry only when all the squares on the opposite direction of PQ will have their mirror image same as that of the square.
So, if they check all the shaded squares in the given figure and if their mirror image is not shaded then we have to shade that.
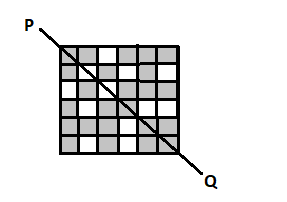
So, now as we can see that in the above figure PQ will be the line of symmetry because all the squares on the opposite side of PQ have their mirror image i.e. the two triangles formed by the line PQ are mirror images of each other.
Now as we had to show the squares which we have shaded to make the line PQ as the line of symmetry.
So, all of the squares that are shared by grey to make line PQ as symmetry line are indicated by brown colour in the figure below.
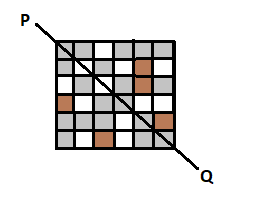
So, the total number of squares filled with brown colour are 5.
Hence, the correct option will be C.
Note: Whenever we come up with this type of problem then we should remember that any line AB will be the line of symmetry if the opposite sides of the line are the mirror images of each other. A mirror image is the image formed when we reflect that image with the mirror. So, here to get the minimum of squares to be shaded so that the line PQ is the line of symmetry we had to shade only those triangles whose mirror images are shaded. This will be the easiest and efficient way to find the solution of the problem.
Complete step-by-step answer:
Now as we know that the mirror image of any shape is the image formed when we reflect the image with the mirror.
And any line will be the line of symmetry if all the images on the opposite side of that line have its mirror image the same as that image if the mirror is the line itself.

Like in the above figure AB will be the line of symmetry because both the triangles on the opposite side of the AB are mirror images of each other and they are identical.
Now as we know that we had to find the minimum number of squares that should be shaded. So, the line PQ became the line of symmetry.
So, PQ will be the line of symmetry only when all the squares on the opposite direction of PQ will have their mirror image same as that of the square.
So, if they check all the shaded squares in the given figure and if their mirror image is not shaded then we have to shade that.

So, now as we can see that in the above figure PQ will be the line of symmetry because all the squares on the opposite side of PQ have their mirror image i.e. the two triangles formed by the line PQ are mirror images of each other.
Now as we had to show the squares which we have shaded to make the line PQ as the line of symmetry.
So, all of the squares that are shared by grey to make line PQ as symmetry line are indicated by brown colour in the figure below.

So, the total number of squares filled with brown colour are 5.
Hence, the correct option will be C.
Note: Whenever we come up with this type of problem then we should remember that any line AB will be the line of symmetry if the opposite sides of the line are the mirror images of each other. A mirror image is the image formed when we reflect that image with the mirror. So, here to get the minimum of squares to be shaded so that the line PQ is the line of symmetry we had to shade only those triangles whose mirror images are shaded. This will be the easiest and efficient way to find the solution of the problem.
Recently Updated Pages
Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

Distinguish between the following Ferrous and nonferrous class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Voters list is known as A Ticket B Nomination form class 9 social science CBSE

Distinguish between Conventional and nonconventional class 9 social science CBSE





