Question

State the name of a regular polygon of 4 sides.
a. Square
b. Trapezium
c. Rectangle
d. Parallelogram

Answer 1

Hint: In order to solve this question, we will consider the properties of regular polygon and will check which of the quadrilateral satisfies all the properties, that will be the correct answer.

Complete step-by-step answer:
We will first see the properties of a regular polygon. So, we know that regular polygons are those which have all the sides of equal length. Also, they have length of every diagonals with $n^{th}$ vertices as constant. And also they have equal angles between each edge of the polygon.
Now, if we consider square, trapezium, rectangle and parallelogram and then consider each property of regular polygon, then the quadrilateral satisfying all the properties will be the correct answer.

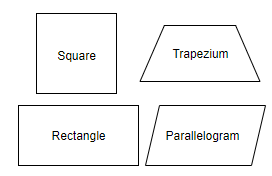
So, we know that all sides of regular polygon are equal and among all the quadrilaterals given, only square has all the sides equal.
We know that the length of every diagonal with the $n^{th}$ vertices is constant. So, square and rectangle both show this property.
We also know that the angles between two consecutive edges are also equal for a regular polygon. So, this condition is true for square and rectangle.
Now, we can see that square is the only quadrilateral which satisfies all the conditions of a regular polygon. Hence, square is the only quadrilateral which is a regular polygon of 4 sides. Therefore, option (a) is the correct answer.

Note: The possible mistake that one can make in this question, is by writing the answer as rectangle instead of square, as one might think that rectangle satisfies all the conditions, but actually rectangle satisfies only 2 out of the 3 conditions, whereas square satisfies all the 3 conditions. So, we need to remember that regular polygon is a polygon which has all the sides of equal length and all diagonals with the $n^{th}$ vertices are of equal length and also, angles between every 2 consecutive edges are equal.