Question

State true or false.
If the angles subtended by the chords of a circle at the center are equal , then the chords are equal.

Answer 1

Hint: It is no surprise that equal chords and equal arcs both subtend equal angles at the centre of a fixed circle. The result for chords can be proven using congruent triangles, but congruent triangles cannot be used for arcs because they are not straight lines, so we need to identify the transformation involved.

Complete step-by-step answer:
Let’s try to figure our relation between length of chord & angle subtended and the center.

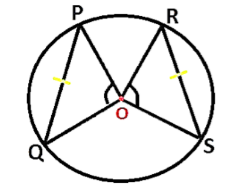
Given: \[\angle SOR{\text{ }} and \angle POQ\] are two equal angles subtended by chords SR and PQ of a circle at its centre O.
Here in the circle, the two chords are given
To Prove : RS = PQ
Proof : In \[\vartriangle SOR{\text{ }} and {\text{ }}\vartriangle POQ\],
OR = OP [Radii of a circle]
OS = OQ [Radii of a circle]
So OP = OS = OQ = OR (all are radii of the circle)
\[\angle SOR{\text{ }} and \angle POQ\] [Given]
Therefore, \[\vartriangle SOR \cong \vartriangle POQ\][By SAS]
Hence, RS = PQ [By cpctc, corresponding parts of congruent triangles are congruent. It means that once two triangles are proven to be congruent, then the three pairs of sides that correspond must be congruent and the three pairs of angles that correspond must be congruent.]
Thus, we conclude that if the angles made by the chords of a circle at the centre are equal, then the chords must be equal.

Note: The converse is also true.
The converse theorem : Equal chords of a circle subtend equal angles at the centre
For convenience, you can use the abbreviation CPCT in place of ‘Corresponding parts of congruent triangles’, and the abbreviation SAS will be used in place of ‘Side-Angle-Side’, because we use this very frequently for proving geometrical problems.