Question

State true or false:
The side opposite to the equal angles of a triangle may be unequal.
a. true
b. false

Answer 1

Hint: Given that Side opposite the equal angles of a triangle may be unequal, we check this statement by considering a triangle and draw a bisector from the unequal angle to divide the triangle into two. Then we can consider the properties of triangles to check the equality of two sides.

Complete step by step solution: Given that Side opposite the equal angles of a triangle may be unequal,
Let us consider a triangle XYZ with equal angles, \[\angle XYZ = \angle YZX\]

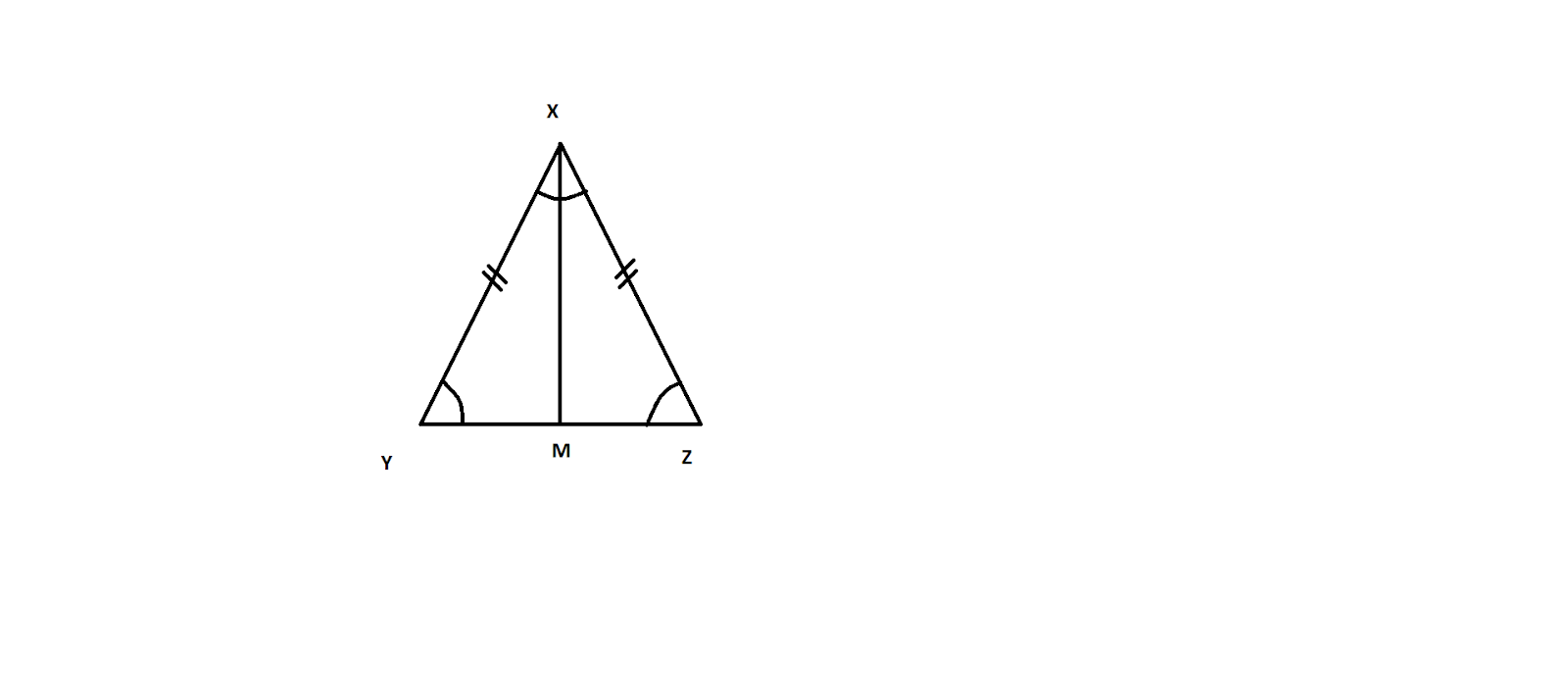
We can draw the angle bisector XM of \[\angle YXZ\] so that it meets YZ at M.
Now let us consider the triangles XMY and XMZ.
Consider the angles, \[\angle XYZ\] and \[\angle YZX\]
It is given that \[\angle XYZ = \angle YZX\] …. (1)
As the side XM is common side for both the triangles, we can write,
 $ \Rightarrow XM = XM$ … (2)
Consider the angles, \[\angle YXM\] and \[\angle ZXM\]
As XM is the bisector of \[\angle YXZ\], they will be equal
 \[\angle YXM = \angle ZXM\] … (3)
Hence, from (1), (2) and (3) by AAS criteria, the triangles XMY and XMZ are congruent.
We know that corresponding parts of congruent triangles will be equal.
We get, \[XY = XZ\]
From the figure XY and XZ are the sides opposite to the equal angles.
So, the side opposite the equal angles of a triangle is equal
So, the given statement is FALSE.

Hence, option (b) is correct.

Note:
Here in the question we have been given that Side opposite the equal angles of a triangle may be unequal, so we can get confused seeing the word ‘maybe’, but as the statement is not sure and as we have proved that Side opposite the equal angles of a triangle is always equal, so we will consider the given statement is false.
The properties of congruence are what we have used here. There are three types of conditions on how we can use the properties of congruence. These are, AAS, SSS, SSA where S denotes the side and A denoting the angle.