
STATEMENT - 1 : If in two triangles, two angles of one triangle are respectively equal to the two angles of the other triangle, then the two triangles are similar.
STATEMENT - 2 : If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio and hence the two triangles are similar.
Find the correct option from the following:
A) Statement – I is True, Statement-2 is True; Statement – 2 is a correct explanation for the Statement – I.
B) Statement – I is True, Statement – 2 is True; Statement – 2 is not a correct explanation for Statement – I.
C) Statement – I is True, Statement – 2 is False.
D) Statement – I is False, Statement – 2 is True.
Answer
494.1k+ views
Hint: We must check the statements first. If both the statements are correct then we must check if there is any relation between the two statements. Finally we must check the options which match the answer.
Complete step-by-step answer:
We have statement 1 as If in two triangles, two angles of one triangle are respectively equal to the two angles of the other triangle, then the two triangles are similar.
First, we will try to find out if it is true or not.
Let’s consider two triangles as follows:
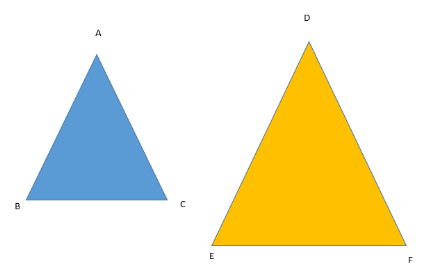
Without loss of generality, let us suppose that $\angle A = \angle D$ and $\angle B = \angle E$ ………(1)
We also know that the sum of all the angles of a triangle results in 180$^ \circ $.
So, \[\angle A{\text{ }} + \angle \;B{\text{ }} + \angle C{\text{ }} = {180^ \circ }\] …….(2) and similarly \[\angle D{\text{ }} + \angle E{\text{ }} + \angle F = {180^ \circ }\]…….(3)
Comparing (2) and (3), we have:-
\[\angle A{\text{ }} + \angle \;B{\text{ }} + \angle C{\text{ }} = \angle D{\text{ }} + \angle E{\text{ }} + \angle F\]
This implies \[\angle A{\text{ }} - \angle D{\text{ }} + \angle \;B{\text{ }} - \angle E{\text{ }} + \angle C{\text{ }} = \angle F\] …….(4)
Using (1) in (4):-
$\angle C = \angle F$
Hence, all the corresponding angles are equal and thus, we have:-
$\vartriangle ABC \sim \vartriangle DEF$
This is because of the AAA similarity rule.
Now, in statement two the reason is different.
Hence, option (A) is discarded and since statement 1 is true, so option (D) is discarded as well.
Now, let us check statement 2.
If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio and hence the two triangles are similar.
This states that in the given triangles $\dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EF}}$.
This is a fact related to similar triangles which we can prove by constructing PQ parallel to EF and then using the theorem that: If a line is drawn parallel to one side of the triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Hence, it is true as well.
Hence, the correct option is (B).
Note: Since the options (A) and (B) are almost similar, we must look at them carefully because we may mistakenly misread them.
We might make the mistake to infer statement 2 as the correct reason because Statement 1 implies statement 2.
We must remember the facts that: sum of all the angles of a triangle results in ${180^ \circ }$ and If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio and hence the two triangles are similar.
Complete step-by-step answer:
We have statement 1 as If in two triangles, two angles of one triangle are respectively equal to the two angles of the other triangle, then the two triangles are similar.
First, we will try to find out if it is true or not.
Let’s consider two triangles as follows:
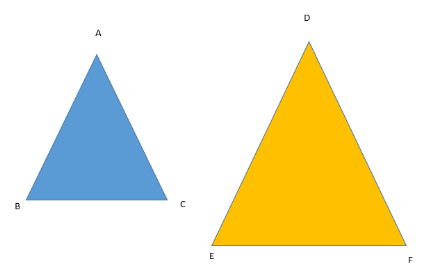
Without loss of generality, let us suppose that $\angle A = \angle D$ and $\angle B = \angle E$ ………(1)
We also know that the sum of all the angles of a triangle results in 180$^ \circ $.
So, \[\angle A{\text{ }} + \angle \;B{\text{ }} + \angle C{\text{ }} = {180^ \circ }\] …….(2) and similarly \[\angle D{\text{ }} + \angle E{\text{ }} + \angle F = {180^ \circ }\]…….(3)
Comparing (2) and (3), we have:-
\[\angle A{\text{ }} + \angle \;B{\text{ }} + \angle C{\text{ }} = \angle D{\text{ }} + \angle E{\text{ }} + \angle F\]
This implies \[\angle A{\text{ }} - \angle D{\text{ }} + \angle \;B{\text{ }} - \angle E{\text{ }} + \angle C{\text{ }} = \angle F\] …….(4)
Using (1) in (4):-
$\angle C = \angle F$
Hence, all the corresponding angles are equal and thus, we have:-
$\vartriangle ABC \sim \vartriangle DEF$
This is because of the AAA similarity rule.
Now, in statement two the reason is different.
Hence, option (A) is discarded and since statement 1 is true, so option (D) is discarded as well.
Now, let us check statement 2.
If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio and hence the two triangles are similar.
This states that in the given triangles $\dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EF}}$.
This is a fact related to similar triangles which we can prove by constructing PQ parallel to EF and then using the theorem that: If a line is drawn parallel to one side of the triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Hence, it is true as well.
Hence, the correct option is (B).
Note: Since the options (A) and (B) are almost similar, we must look at them carefully because we may mistakenly misread them.
We might make the mistake to infer statement 2 as the correct reason because Statement 1 implies statement 2.
We must remember the facts that: sum of all the angles of a triangle results in ${180^ \circ }$ and If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio and hence the two triangles are similar.
Recently Updated Pages
The correct geometry and hybridization for XeF4 are class 11 chemistry CBSE

Water softening by Clarks process uses ACalcium bicarbonate class 11 chemistry CBSE

With reference to graphite and diamond which of the class 11 chemistry CBSE

A certain household has consumed 250 units of energy class 11 physics CBSE

The lightest metal known is A beryllium B lithium C class 11 chemistry CBSE

What is the formula mass of the iodine molecule class 11 chemistry CBSE

Trending doubts
Draw an outline map of India and mark the following class 9 social science CBSE

Write a short note on The Shiwalik Range class 9 social science CBSE

What is chronic hunger and seasonal hunger

Give the formula for class mark and class size of a class 9 maths CBSE

The radius of the base of a cone is 5 cm and its height class 9 maths CBSE

How to find xi in statistics class 9 maths CBSE




