Answer
468.6k+ views
Hint: There is a problem to find the probability that land inside the circle with diameter \[1m\]
Probability is a type of ratio where we compare how many times an outcome can occur compared to all possible outcomes.
\[{\text{Probability = }}\dfrac{{\left( {{\text{The number of wanted outcomes}}} \right)}}{{\left( {{\text{The number of possible outcomes}}} \right)}}\]
Complete step-by-step answer:
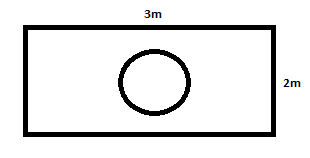
The given figure is:
It is given that a die is dropped at random on the rectangular region shown in fig.
We need to determine the probability that it will land inside the circle with diameter \[1m\].
Here we use the area to find the probability.
Now we have the diameter of the circle is \[1m\].
Thus we get the radius of the circle is \[\dfrac{1}{2}m\] .
The area of the circle is
\[ \Rightarrow \pi {r^2}\]
Substituting the values in given,
\[ \Rightarrow \dfrac{{22}}{7} \times \dfrac{1}{2} \times \dfrac{1}{2}\]
\[ \Rightarrow \dfrac{{11}}{{14}}{m^2}\]
Again it is given that,
The length of the rectangle is \[3m\].
The breadth of the rectangle is \[2m\].
Thus the area of the rectangle is =\[3 \times 2 = 6{m^2}\]
Probability (P) that the die will land inside the circle
\[ \Rightarrow \dfrac{{\left( {{\text{The number of wanted outcomes}}} \right)}}{{\left( {{\text{The number of possible outcomes}}} \right)}}\]
Probability formula for the problem can be written as,
\[ \Rightarrow \dfrac{{{\text{The area of the circle}}}}{{{\text{the area of the rectangle}}}}\]
\[ \Rightarrow \dfrac{{\dfrac{{11}}{{14}}}}{{\dfrac{6}{1}}}\]
Simplifying we get,
\[ \Rightarrow \dfrac{{11}}{{14}} \times \dfrac{1}{6}\]
\[ \Rightarrow \dfrac{{11}}{{84}}\]
Hence we get, the probability that the die will land inside the circle with diameter \[1m\] is\[\dfrac{{11}}{{84}}\].
Note: A rectangle is a 2D shape in geometry, having four sides and four corners. Its two sides meet at right angles. Thus, a rectangle has four angles, each measuring \[90^\circ \]. The opposite sides of a rectangle have the same lengths and are parallel.
\[{\text{Area of the rectangle}}\] = \[Length \times breadth\]
A circle is a shape consisting of all points in a plane that are a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant.
Area of the circle is \[\pi {r^2}\].
Probability is a type of ratio where we compare how many times an outcome can occur compared to all possible outcomes.
\[{\text{Probability = }}\dfrac{{\left( {{\text{The number of wanted outcomes}}} \right)}}{{\left( {{\text{The number of possible outcomes}}} \right)}}\]
Complete step-by-step answer:
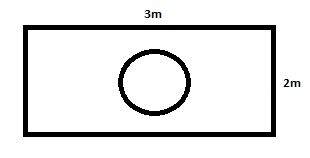
The given figure is:

It is given that a die is dropped at random on the rectangular region shown in fig.
We need to determine the probability that it will land inside the circle with diameter \[1m\].
Here we use the area to find the probability.
Now we have the diameter of the circle is \[1m\].
Thus we get the radius of the circle is \[\dfrac{1}{2}m\] .
The area of the circle is
\[ \Rightarrow \pi {r^2}\]
Substituting the values in given,
\[ \Rightarrow \dfrac{{22}}{7} \times \dfrac{1}{2} \times \dfrac{1}{2}\]
\[ \Rightarrow \dfrac{{11}}{{14}}{m^2}\]
Again it is given that,
The length of the rectangle is \[3m\].
The breadth of the rectangle is \[2m\].
Thus the area of the rectangle is =\[3 \times 2 = 6{m^2}\]
Probability (P) that the die will land inside the circle
\[ \Rightarrow \dfrac{{\left( {{\text{The number of wanted outcomes}}} \right)}}{{\left( {{\text{The number of possible outcomes}}} \right)}}\]
Probability formula for the problem can be written as,
\[ \Rightarrow \dfrac{{{\text{The area of the circle}}}}{{{\text{the area of the rectangle}}}}\]
\[ \Rightarrow \dfrac{{\dfrac{{11}}{{14}}}}{{\dfrac{6}{1}}}\]
Simplifying we get,
\[ \Rightarrow \dfrac{{11}}{{14}} \times \dfrac{1}{6}\]
\[ \Rightarrow \dfrac{{11}}{{84}}\]
Hence we get, the probability that the die will land inside the circle with diameter \[1m\] is\[\dfrac{{11}}{{84}}\].
Note: A rectangle is a 2D shape in geometry, having four sides and four corners. Its two sides meet at right angles. Thus, a rectangle has four angles, each measuring \[90^\circ \]. The opposite sides of a rectangle have the same lengths and are parallel.
\[{\text{Area of the rectangle}}\] = \[Length \times breadth\]
A circle is a shape consisting of all points in a plane that are a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant.
Area of the circle is \[\pi {r^2}\].
Recently Updated Pages
A particle is undergoing a horizontal circle of radius class 11 physics CBSE

A particle is thrown vertically upwards with a velocity class 11 physics CBSE

A particle is rotated in a vertical circle by connecting class 11 physics CBSE

A particle is projected with a velocity v such that class 11 physics CBSE

A particle is projected with a velocity u making an class 11 physics CBSE

A particle is projected vertically upwards and it reaches class 11 physics CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Which is the largest saltwater lake in India A Chilika class 8 social science CBSE

Ghatikas during the period of Satavahanas were aHospitals class 6 social science CBSE