Question

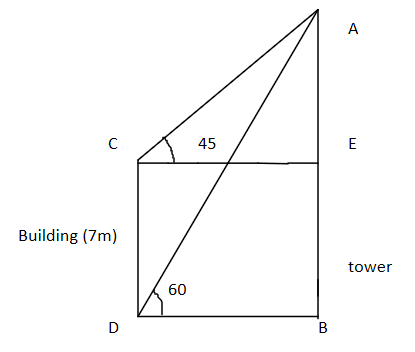
The angle of depression of the top and the bottom of a 7m tall building from the top of tower are ${45^ \circ }$ and ${60^ \circ }$ respectively, find the height of the tower.

Answer 1

Hint: By looking at the given figure we can clearly see the right angled triangle AEC and ABD. And we have to find the length of AB, also the length of the CD is given to us.
We will use suitable trigonometric functions for each of the triangles and then solving the equation formed, we will get required length.

Complete step-by-step answer:
Given angle of depression of top of the building from top of tower is ${45^ \circ }$,
And the angle of depression of the bottom of the building from top of tower is ${60^ \circ }$.
Let the height of the tower be h.
Length of the building is $CD = 7m$ -(1)
Now,
$AE = AB - EB$
As, $EB = CD$,
$AE = h - CD$
Using (1),
$AE = h - 7$ -(2)
Now from the above figure we can see a right-angled triangle AEC-
Therefore,

$
  \tan \theta = \dfrac{{perpendicular}}{{base}} \\
  \tan {45^ \circ } = \dfrac{{AE}}{{CE}} \\
 $
Using $\tan {45^ \circ } = 1$ and (2) equation,
$1 = \dfrac{{h - 7}}{{BD}}$
$BD = h - 7$ -(3)
Now we can also see the right-angled triangle ABD-
So,
$\tan {60^ \circ } = \dfrac{{AB}}{{BD}}$
Using $\tan {60^ \circ } = \sqrt 3 $ and (3) equation,
$
  \sqrt 3 = \dfrac{h}{{h - 7}} \\
  \sqrt 3 h - 7\sqrt 3 = h \\
  \sqrt 3 h - h = 7\sqrt 3 \\
  h\left( {\sqrt 3 - 1} \right) = 7\sqrt 3 \\
  h = \dfrac{{7\sqrt 3 }}{{\sqrt 3 - 1}}m \\
 $
Therefore, the height of the tower is $\dfrac{{7\sqrt 3 }}{{\sqrt 3 - 1}}$m.

Note: In the above question we have used $\tan \theta $ because if we see the diagram there are two right-angled triangles formed with bases of equal length, perpendicular is required and the corresponding angles are given.
Hence, we need a trigonometric function including base and perpendicular which is $\tan \theta $.
Also, we can rationalize the final answer and we will obtain height of tower equal to-
$\dfrac{{7\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{2}$.