Question

The angle of elevation of the top of a tower standing on a horizontal plane from two points on a line passing through the foot of the tower at a distance 9 ft. and 16 ft. respectively are complementary angles. Then the height of the tower is:
A. 9 ft.
B. 12 ft.
C. 16 ft.
D. 144 ft.

Answer 1

Hint: Here, we will first draw the triangle using the given conditions to simplify the calculation. Then use the tangential property, that is, \[\tan {\text{A}} = \dfrac{p}{b}\], where \[p\] is the perpendicular and \[b\] is the base. Apply this property, and then use the given conditions to find the required value.

Complete step by step answer:

Let us assume that the height of the tower is \[h\].

We are given that the angle of elevation of the top of a tower standing on a horizontal plane from two points on a line passing through the foot of the tower at a distance 9 ft. and 16 ft. respectively are complementary angles.

First, we will draw the triangle using the given conditions.

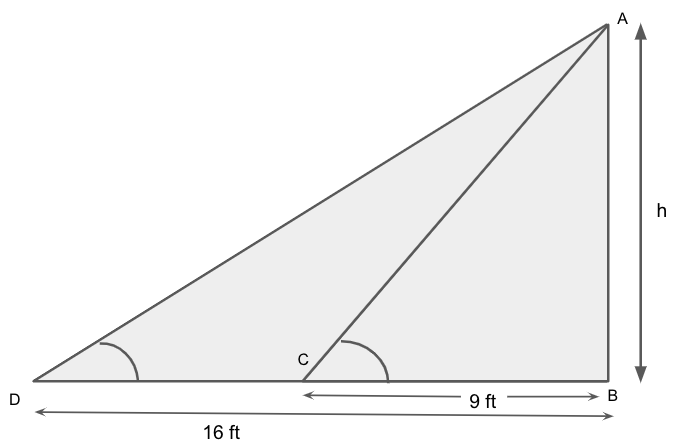
Let us also assume that \[\angle {\text{ADB}}\] is \[\alpha \] and \[\angle {\text{ACB}}\] is \[\beta \].

First, we will take the triangle \[\Delta {\text{ABD}}\].
We will use the tangential property, that is, \[\tan {\text{D}} = \dfrac{p}{b}\], where \[p\] is the perpendicular and \[b\] is the base.

Using the above tangential property, we get

\[\tan \alpha = \dfrac{{{\text{AB}}}}{{{\text{BD}}}}\]

Substituting the values of the length AB and BD in the above equation, we get

\[ \Rightarrow \tan \alpha = \dfrac{h}{{16}}{\text{ ......eq.}}\left( 1 \right)\]

We will now take the triangle \[\Delta {\text{ABC}}\],

We will use the tangential property, that is, \[\tan {\text{C}} = \dfrac{p}{b}\], where \[p\] is the perpendicular and \[b\] is the base.

Using the above tangential property, we get

\[\tan \beta = \dfrac{{{\text{AB}}}}{{{\text{BC}}}}\]

Substituting the values of the length AB and BC in the above equation, we get

\[ \Rightarrow \tan \beta = \dfrac{h}{9}{\text{ ......eq.}}\left( 2 \right)\]

Since \[\angle {\text{ACB}}\] and \[\angle {\text{ADB}}\] are complementary angles, the sum of \[\alpha \] and \[\beta \] is 90 degrees.

Then, we have

\[
   \Rightarrow \alpha + \beta = 90 \\
   \Rightarrow \beta = 90 - \alpha \\
 \]

Substituting this value of \[\beta \] in equation \[\left( 2 \right)\], we get

\[
   \Rightarrow \tan \left( {90 - \alpha } \right) = \dfrac{h}{{16}} \\
   \Rightarrow \cot \alpha = \dfrac{h}{{16}} \\
   \Rightarrow \tan \alpha = \dfrac{{16}}{h}{\text{ ......eq.}}\left( 3 \right) \\
 \]

From equation \[\left( 1 \right)\] and equation \[\left( 3 \right)\], we get

\[ \Rightarrow \dfrac{h}{9} = \dfrac{{16}}{h}\]

Cross-multiplying in the above equation, we get
\[
   \Rightarrow {h^2} = 16 \times 9 \\
   \Rightarrow {h^2} = 144 \\
 \]

Taking square root in the above equation on both sides, we get
\[
   \Rightarrow h = \pm \sqrt {144} \\
   \Rightarrow h = \pm 12 \\
 \]

Since the value of height can never be negative, the negative value of \[h\] is discarded.

Thus, the height of the tower is 12 ft.

Hence, option B is correct.


Note: In solving these types of questions, you should be familiar with the concept of angle of depression and the tangential properties. Students should make the diagram for better understanding. Using the values of respective angles you can simply find any length present in the figure using the tangential value ‘\[\tan \]’, which makes our problem easy to solve. Students need to write the units in the final answer or else the answer will be partially wrong.