Question

The angle of friction between two surfaces is \[{{37}^{0}}\], if \[\cos {{37}^{0}}=\dfrac{4}{5}\], coefficient of static friction between those two surfaces is –
\[\begin{align}
  & \text{A) }\dfrac{3}{4} \\
 & \text{B) }\dfrac{4}{3} \\
 & \text{C) }\dfrac{3}{5} \\
 & \text{D) }\dfrac{5}{3} \\
\end{align}\]

Answer 1

Hint: We need to find the relation between the frictional parameters and the angle between the surfaces in contact that results in the friction to come into play. These relations will help us find the required coefficient of friction for this problem.

Complete Step-by-Step Solution:
We are given that two surfaces experience a frictional force. We know that any contact between two surfaces can result in frictional force. The coefficient of the frictional force is defined as the tangent of the angle between the contacts of the two surfaces.

We are given two surfaces which are in contact with each other at an angle of \[{{37}^{0}}\].

The coefficient of friction for these surfaces can be given as –
\[\begin{align}
  & \mu =\tan \theta \\
 & \therefore \mu =\tan {{37}^{0}} \\
\end{align}\]
Where \[\mu \] is the coefficient of friction.

We are given the cosine of the angle. We know that we can find the tangent of the same angle from the cosines using simple trigonometric relations or the triangular relations.

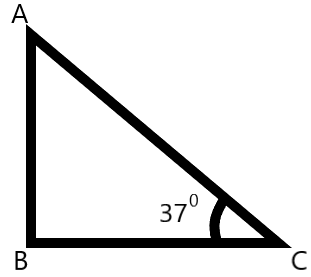
Consider the triangle ABC,
\[\begin{align}
  & \Delta ABC, \\
 & \cos \angle BCA=\cos {{37}^{0}} \\
 & \therefore \dfrac{BC}{AC}=\dfrac{4}{5} \\
\end{align}\]

Now, we can use the Pythagoras theorem to find the side AB as –
\[\begin{align}
  & A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}} \\
 & \Rightarrow AB=\sqrt{A{{C}^{2}}+B{{C}^{2}}} \\
 & \Rightarrow AB=\sqrt{{{5}^{2}}+{{4}^{2}}} \\
 & \therefore AB=3units \\
\end{align}\]

Now, we can find the tangent of the required angle as –
\[\begin{align}
  & \tan \theta =\tan {{37}^{0}} \\
 & \Rightarrow \mu =\tan {{37}^{0}}=\dfrac{AB}{BC} \\
 & \therefore \mu =\dfrac{3}{4} \\
\end{align}\]
So, the coefficient of friction between the two surfaces inclined at an angle of \[{{37}^{0}}\] is found to be \[\dfrac{3}{4}\].
This is the required solution for this problem.

The correct answer is given by option A.

Note:
The coefficient of friction is often considered a constant quantity for two given pairs of surfaces. When one among the two surfaces is fixed such as the floor, the coefficient of friction is considered irrespective of the object sliding over in a perpendicular direction.