
The angles of a pentagon in degrees are
Answer
503.4k+ views
Hint: To solve the given question, we will first find out what a pentagon is. Then, we will find out the sum of the interior angles in the pentagon with the help of the formula:
Complete step-by-step answer:
Before we solve the question, we will first find out what kind of polygon is a pentagon. A pentagon is a polygon having five sides or edges and five angles. The angles may or may not be equal. In our case, there are five angles of the pentagon of which all are different so the given pentagon is an irregular pentagon.
Let us draw a representative figure of pentagon and all the angles as shown below,
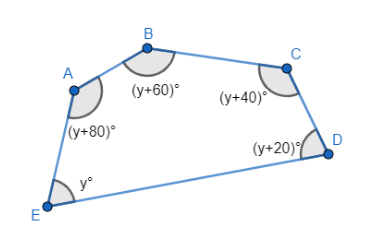
Now, we will find the sum of interior angles in a pentagon. The sum of interior angles in a polygon with n sides is given by the formula,
In our case, n = 5, so we will get,
Now, the angles which are given in the question should have the sum equal to the sum of interior angles. Thus, we can say that,
Now, we have to find the smallest angle of the pentagon. Among the five angles given in the pentagon, the smallest angle us y. So, the smallest angle of the pentagon will be
Note: We can also proceed in an alternate way after finding the sum of the interior angles as
Thus, we have,
Complete step-by-step answer:
Before we solve the question, we will first find out what kind of polygon is a pentagon. A pentagon is a polygon having five sides or edges and five angles. The angles may or may not be equal. In our case, there are five angles of the pentagon of which all are different so the given pentagon is an irregular pentagon.
Let us draw a representative figure of pentagon and all the angles as shown below,

Now, we will find the sum of interior angles in a pentagon. The sum of interior angles in a polygon with n sides is given by the formula,
In our case, n = 5, so we will get,
Now, the angles which are given in the question should have the sum equal to the sum of interior angles. Thus, we can say that,
Now, we have to find the smallest angle of the pentagon. Among the five angles given in the pentagon, the smallest angle us y. So, the smallest angle of the pentagon will be
Note: We can also proceed in an alternate way after finding the sum of the interior angles as
Thus, we have,
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

The first successful textile mill was established in class 9 social science CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE





