Question

The base of an isosceles triangle is 24 cm and its area is 192 sq. cm. Find its perimeter.
(a) 64 cm
(b) 60 cm
(c) 63 cm
(d) 62 cm

Answer 1

Hint: Here, we need to find the perimeter of the given isosceles triangle. First, we will use the formula for the area of a triangle to find the height of the triangle. Then, we will use congruence and Pythagoras’s theorem to find the lengths of the remaining sides of the triangle. Finally, we will add the sides of the triangle to find the perimeter of the isosceles triangle.

Formula Used:
We will use following formulas:
1.The area of a triangle is given by the formula \[\dfrac{1}{2}bh\], where \[b\] is the base of the triangle, and \[h\] is the height of the triangle.
2.The Pythagoras’s theorem states that the square of the hypotenuse of a right angled triangle is equal to the sum of squares of the other two sides, that is \[{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Perpendicula}}{{\rm{r}}^2} + {\rm{Bas}}{{\rm{e}}^2}\].
3.The perimeter of a triangle is the sum of all of its three sides.

Complete step-by-step answer:
First, we will draw the figure using the given information, showing the height of the triangle.

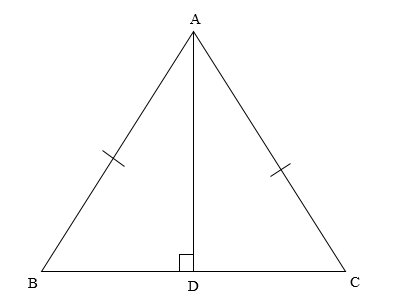
Here, ABC is the given isosceles triangle. AB and AC are the equal sides of the triangle, and BC is the base of length 24 cm. The line segment AD is the height of the triangle ABC.
Now, the area of a triangle is given by the formula \[\dfrac{1}{2}bh\], where \[b\] is the base of the triangle, and \[h\] is the height of the triangle.
Thus, we get
Area of triangle ABC \[ = \dfrac{1}{2} \times BC \times AD\]
Substituting \[BC = 24\] cm in the equation, we get
\[ \Rightarrow \] Area of triangle ABC \[ = \dfrac{1}{2} \times 24 \times AD\]
Simplifying the expression, we get
\[ \Rightarrow \] Area of triangle ABC \[ = 12AD\]
It is given that the area of the triangle is 192 sq. cm.
Therefore, we get
\[ \Rightarrow 12AD = 192\]
Dividing both sides of the equation by 12, we get
\[ \Rightarrow AD = 16\]
Thus, we get the height of the triangle as 16 cm.
Now, since AD is the height of the triangle ABC, we have \[\angle ADB = \angle ADC = 90^\circ \].
In \[\Delta ADB\] and \[\Delta ADC\], we have
\[AB = AC\] (Equal sides of an isosceles triangle)
\[AD = AD\] (Common side)
\[\angle ADB = \angle ADC = 90^\circ \]
Therefore, by R.H.S. congruency criterion, we have proved that triangles \[\Delta ADB\] and \[\Delta ADC\] are congruent.
We know that congruent parts of two congruent triangles are equal.
Since \[\Delta ADB\] and \[\Delta ADC\] are congruent, we get
\[DB = DC\]
From the figure, we can observe that the side BC is the sum of the line segments DB and DC.
Thus, we get
\[ \Rightarrow DB + DC = BC\]
Substituting \[DB = DC\] and \[BC = 24\] cm in the equation, we get
\[ \Rightarrow DC + DC = 24\]
Adding the terms in the expression, we get
\[ \Rightarrow 2DC = 24\]
Dividing both sides of the equation by 2, we get
\[ \Rightarrow DC = 12\]
Thus, we get
\[ \Rightarrow DB = DC = 12\] cm
Now, we will use the Pythagoras’s theorem in the right angled triangle ADB.
From the figure, we can observe that AD is the perpendicular, DB is the base, and AB is the hypotenuse of the right angled triangle ADB.
Therefore, using the Pythagoras’s theorem in right angled triangle ADB, we get
\[A{B^2} = A{D^2} + D{B^2}\]
Substituting \[DB = 12\] cm and \[AD = 16\] cm in the equation, we get
\[ \Rightarrow A{B^2} = {16^2} + {12^2}\]
Applying the exponents on the bases, we get
\[ \Rightarrow A{B^2} = 256 + 144\]
Adding the terms in the expression, we get
\[ \Rightarrow A{B^2} = 400\]
Taking the square root of both sides, we get
\[ \Rightarrow AB = 20\] cm
Thus, we get
\[ \Rightarrow AB = AC = 20\] cm
Therefore, we get the sides of the isosceles triangle as 20 cm, 20 cm, and 24 cm.
Finally, we will calculate the perimeter of the triangle ABC.
The perimeter of a triangle is the sum of all of its three sides.
Therefore, we get
Perimeter of triangle ABC \[ = AB + BC + AC\]
Substituting \[AB = AC = 20\] cm and \[BC = 24\] cm in the equation, we get
\[ \Rightarrow \] Perimeter of triangle ABC \[ = 20 + 24 + 20\]
Adding the terms, we get
\[ \Rightarrow \] Perimeter of triangle ABC \[ = 64\]
Therefore, we get the perimeter of the given isosceles triangle as 64 cm.
Thus, the correct option is option (a).
Note: We used the R.H.S. congruence criterion to prove that \[\Delta ADB \cong \Delta ADC\]. According to the R.H.S. congruence criterion, if in two right angled triangles, the corresponding hypotenuse, and any of the two corresponding sides are equal, then the two triangles are congruent. Also, Pythagoras theorem is only applied to right angled triangles.