Question

The bisector of an angle is produced backwards. It bisects which angle at the same vertex?
(a) Acute
(b) Obtuse
(c) Reflex
(d) Complete

Answer 1

Hint: Let us take the figure of the given information that is the angular bisector of an angle as shown below.

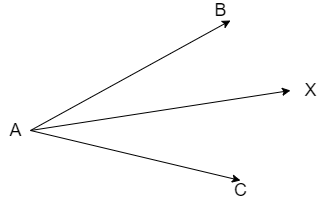
We solve this problem by producing the ray AX backwards and we find the angle which it bisects other than angle \[\angle BAC\] by using the definition of angular bisector.
The angular bisector of an angle is the line that divides the angle into two equal angles.
We also use the condition that the sum of all angles at a point on a straight line equal to \[{{180}^{\circ }}\]
We use the condition that the exterior angle of an acute angle is an obtuse angle and vice versa.

Complete step by step answer:
Let us assume that there is an angular bisector AX of acute angle \[\angle BAC\]
We know that the exterior angle of an acute angle is an obtuse angle and vice versa.
So, we can say that the exterior angle \[ext\left( \angle BAC \right)\] is an obtuse angle.
We know that the angular bisector of an angle is the line that divides the angle into two equal angles.
Now, by using the above definition to angle \[\angle BAC\] we get
\[\Rightarrow \angle BAX=\angle XAC\]
Now, let us produce the ray AX backwards then we get

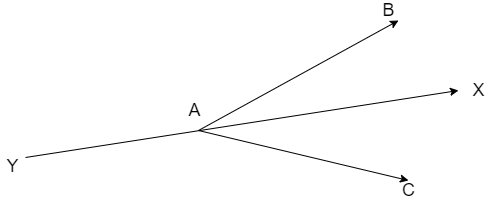
Here we can see that the produced ray AX divides the exterior angle \[ext\left( \angle BAC \right)\]
Now, let us check whether the ray AY divides the exterior angle \[ext\left( \angle BAC \right)\]
We know that the condition that the sum of all angles at a point on a straight line equal to \[{{180}^{\circ }}\]
Now, by using the above condition to the straight line YX we get two conditions as
\[\Rightarrow \angle BAX+\angle BAY={{180}^{\circ }}......equation(i)\]
\[\Rightarrow \angle XAC+\angle CAY={{180}^{\circ }}......equation(ii)\]
Now, by subtracting the equation (ii) from the equation (i) we get
\[\begin{align}
  & \Rightarrow \left( \angle BAX+\angle BAY \right)-\left( \angle XAC+\angle CAY \right)={{180}^{\circ }}-{{180}^{\circ }} \\
 & \Rightarrow \left( \angle BAY-\angle CAY \right)+\left( \angle BAX-\angle XAC \right)=0 \\
\end{align}\]
Now, by substituting the value that is \[\angle BAX=\angle XAC\] in above equation we get
\[\begin{align}
  & \Rightarrow \left( \angle BAY-\angle CAY \right)=0 \\
 & \Rightarrow \angle BAY=\angle CAY \\
\end{align}\]
Now, by using the definition of an angular bisector we can conclude that the ray AY divides the exterior angle \[ext\left( \angle BAC \right)\] in two equal parts.
So, we can say that the ray AY is the angular bisector of exterior angle \[ext\left( \angle BAC \right)\]
Therefore, we can conclude that the angular bisector produced backwards bisects the obtuse angle at the same vertex.

So, the correct answer is “Option b”.

Note: Students may make mistakes in taking the given question into figure.
We are not given the nature of the original angle, that is we are not mentioned whether the initial angle is acute or obtuse.
In that case we take the general condition that the angle as acute angle then we get the figure as

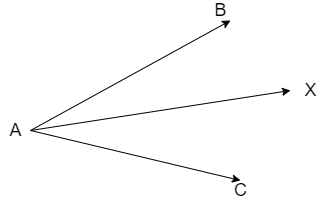
But students may take the initial angle as obtuse angle and take the figure as

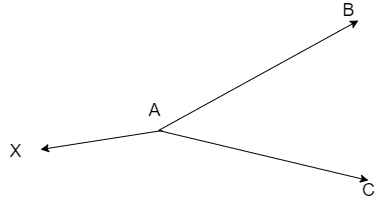
Here, it is assumed that the ray AX is angular bisector of exterior angle \[ext\left( \angle BAC \right)\]
But we need to assume the first condition because it is the standard condition that when we do not mention any nature of angle we assume it as acute angle.