Question

The $\text{ C}-\text{C }$ bond length is maximum in:
A) Graphite
B) $\text{ }{{\text{C}}_{\text{70}}}\text{ }$
C) Diamond
D) $\text{ }{{\text{C}}_{\text{60}}}\text{ }$

Answer 1

Hint: carbon has a property of catenation and thus exhibits various allotropes. Allotropes are the compound of a single element that may differ in chemical and physical properties. Carbon has various allotropes such as graphite, diamond, buckminsterfullerene or C-60, etc. These allotropes are entirely made of the carbon atom, but have a difference in the hybridization of carbon. In graphite, C-60 carbon is found to be $\text{s}{{\text{p}}^{2}}$ hybridized, while in diamond it is $\text{s}{{\text{p}}^{3}}$ hybridized. Hybridization has a significant effect on the properties.

Complete step by step solution:
The term allotrope refers to one or more physical forms of a chemical element that occurs in the same physical state. Allotropes may show differences in chemical and physical properties.
The carbon has a property to form a bond with another carbon atom. This is called catenation. Due to this carbon exhibits allotropy. The allotropes of carbon as:
1. Graphite
2. Diamond
3. Buckminsterfullerene
One of the well-known allotropes of carbon is diamond.
It is the pure crystalline allotrope of carbon. In diamond, each carbon is linked to four neighbouring carbon atoms as seen in the figure below. Since it is forming four bonds, the carbon is $\text{s}{{\text{p}}^{\text{3}}}$ hybridized. Thus, carbons are linked tetrahedrally.
We know that the bond lengths between the atoms depend on the hybridization, which is on the percentage s character of the hybridized orbital. The s character is inversely related to the bond length. As a character increases, bond length decreases.
The carbon atoms in the diamond are $\text{s}{{\text{p}}^{\text{3}}}$ hybridized. , let total contribution by the hybrid orbitals be $\text{ 100 }{\scriptstyle{}^{0}/{}_{0}}\text{ }$. Then ones and three orbitals will contribute towards the hybridization. The extent of hybridization offered by the s orbitals would be,
$\begin{align}
& \text{ }~100{\scriptstyle{}^{0}/{}_{0}}\text{ = Contribution of 3 p-orbitals + Contribution of 1 s-orbitals} \\
& \Rightarrow \text{ }100{\scriptstyle{}^{0}/{}_{0}}\text{ = 4}\times \text{Contribution of 1 orbitals} \\
& \therefore \text{Contribution of 1 orbitals = }\dfrac{100{\scriptstyle{}^{0}/{}_{0}}}{\text{4}}\text{ = 25}{\scriptstyle{}^{0}/{}_{0}} \\
\end{align}$
Thus, 3 p orbitals contribute total $\text{ 75}{\scriptstyle{}^{0}/{}_{0}}\text{ }$ towards the bond, and one orbital contributes only $\text{25}{\scriptstyle{}^{0}/{}_{0}}$. we know that,
$\text{ Bond length }\propto \text{ }\dfrac{1}{\text{s-character}}\text{ }$
Thus, it is found that the carbon-carbon bond diamond has the maximum bond length.
However, in graphite,$\text{ }{{\text{C}}_{\text{60}}}\text{ }$ or $\text{ }{{\text{C}}_{\text{70}}}\text{ }$the carbon is $\text{s}{{\text{p}}^{2}}$ hybridized. Here, s character is found to be equal to $\text{ 33}{\scriptstyle{}^{0}/{}_{0}}\text{ }$, which is greater than the diamond. Thus, for graphite,$\text{ }{{\text{C}}_{\text{60}}}\text{ }$ or $\text{ }{{\text{C}}_{\text{70}}}\text{ }$ the bond length is less than that of the diamond.

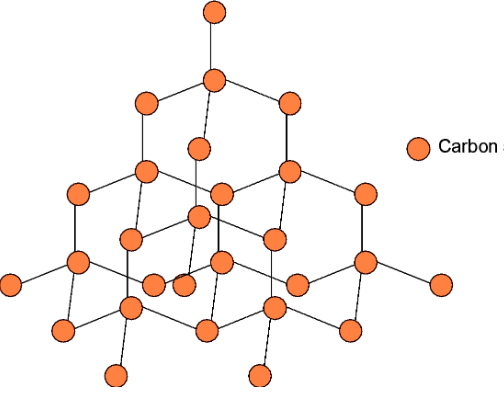
Diamond is an extremely hard allotrope of carbon. This is because the rupturing of a large number of covalent bonds requires a huge amount of energy. This breaking is not an easy task, which makes the diamond the hardest allotropes of carbon on earth.
Thus, here we know that diamonds have a maximum carbon-carbon bond.

Hence, (C) is the correct option.

Note: Note that s orbitals are closer to the nucleus than the p orbital. We can say that, if p-orbitals contribute more than the atoms forming a bond are away from each other this in case increase the distance between atoms. Therefore we can say the bond order is directly related to the p-character.
However, for $\text{ s}{{\text{p}}^{\text{2}}}$ and $\text{ sp }$ orbitals the s character is $\text{ 33}{\scriptstyle{}^{0}/{}_{0}}\text{ }$and $\text{ 50}{\scriptstyle{}^{0}/{}_{0}}\text{ }$ respectively and close to nucleus thus have short bond length but forms multiple bonds.