Question

The circle OAB where O is origin and A, B are points on the coordinate axes is drawn such that the distances of points A and B from the tangent to the circle at origin are p and q respectively. Prove that the diameter of the circle is ‘p + q’ and its center is$\left[ {\dfrac{1}{2}\sqrt {{\text{p}}\left( {{\text{p + q}}} \right)} ,\dfrac{1}{2}\sqrt {{\text{q}}\left( {{\text{p + q}}} \right)} } \right]$.

Answer 1

Hint: To prove the diameter and the center of the circle, we consider a general equation of a circle and find the tangent equation to it at the origin. Then we find the distance of this tangent to points A and B. Then we find the diameter of the circle and find the midpoint of the diameter to find the center of the circle.

Complete step by step answer:
Given Data,
OAB is a circle, A and B are points on the coordinate axis.

To prove,
Diameter = p + q
Center = $\left[ {\dfrac{1}{2}\sqrt {{\text{p}}\left( {{\text{p + q}}} \right)} ,\dfrac{1}{2}\sqrt {{\text{q}}\left( {{\text{p + q}}} \right)} } \right]$

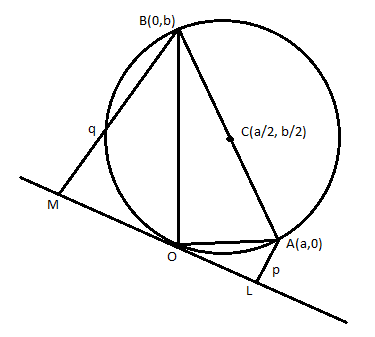
Let us consider a circle with center at point C along with points A and B on the coordinate axis with a tangent of the circle passing through the origin and touching the circle at the origin O itself.
We draw an appropriate figure which looks as follows:

We have to find the diameter of the circle AB from the figure and the center of circle C.
Given the distance from the tangent to the point B is q and the distance from the tangent to the point A is p.

Let us consider the equation of circle be in the general form of a circle equation which is given as,
${{\text{x}}^2} + {{\text{y}}^2} - {\text{ax - by = 0}}$

Now we know the equation of a tangent from the circle is given by the formula,
ax + by = 0 (∵ The tangent touches the circle at the origin)

The formula of perpendicular distance from a point (m, n) to a line px + qy + c = 0 is given by,
${\text{d = }}\dfrac{{|{\text{pm + qn + c|}}}}{{\sqrt {{{\text{p}}^2} + {{\text{q}}^2}} }}$
Now given the distance from the tangent to the point A (a, 0) is p and the equation of tangent is ax + by = 0.
Therefore, ${\text{p = }}\dfrac{{{{\text{a}}^2}}}{{\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} }}$
Now given the distance from the tangent to the point B (0, b) is q and the equation of tangent is ax + by = 0.
Therefore, ${\text{q = }}\dfrac{{{{\text{b}}^2}}}{{\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} }}$
Now that we have the values of p and q let us compute ‘p + q’,
$
   \Rightarrow {\text{p + q = }}\dfrac{{{{\text{a}}^2}}}{{\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} }} + \dfrac{{{{\text{b}}^2}}}{{\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} }} \\
   \Rightarrow {\text{p + q = }}\dfrac{{{{\text{a}}^2} + {{\text{b}}^2}}}{{\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} }} \\
   \Rightarrow {\text{p + q = }}\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} \\
$

From the figure let us consider the line joining points A (a, 0) and B (0, b). Using the formula of distance between two points we compute the length of AB which is also the diameter of the circle,
${\text{AB = }}\sqrt {{{\left( {{\text{a - 0}}} \right)}^2} + {{\left( {0 - {\text{b}}} \right)}^2}} = \sqrt {{{\text{a}}^2} + {{\text{b}}^2}} $
Hence the length of diameter AB is equal to p + q
Therefore the diameter of the circle is ‘p + q’

Now from the above we have the values,
${\text{p = }}\dfrac{{{{\text{a}}^2}}}{{\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} }}$, ${\text{q = }}\dfrac{{{{\text{b}}^2}}}{{\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} }}$and ${\text{p + q = }}\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} $
Using these terms we can compute the values of a and b which are,
${{\text{a}}^2} = {\text{p}}\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} \Rightarrow {\text{a = }}\sqrt {{\text{p}}\left( {{\text{p + q}}} \right)} $
${{\text{b}}^2} = {\text{q}}\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} \Rightarrow {\text{b = }}\sqrt {{\text{q}}\left( {{\text{p + q}}} \right)} $

From the figure the diameter of the circle is AB = p + q, therefore we can deduce the midpoint of AB or the center of circle is$\left( {\dfrac{{\text{a}}}{2},\dfrac{{\text{b}}}{2}} \right)$.
Therefore, $\left( {\dfrac{{\text{a}}}{2},\dfrac{{\text{b}}}{2}} \right) = \left( {\dfrac{1}{2}\sqrt {{\text{p}}\left( {{\text{p + q}}} \right)} ,\dfrac{1}{2}\sqrt {{\text{q}}\left( {{\text{p + q}}} \right)} } \right)$is the midpoint of the circle.
Hence proved.


Note: In order to solve this type of problems the key is to know the concept of circles along with their tangents and other geometrical concepts like distance between a line and a point, distance between two points and midpoint of two points.
We use the respective formulae of all these concepts to prove the given in the question. Being able to write the tangent equation to the circle is the key to solve this problem. From then everything is pretty straightforward.
We draw an appropriate diagram to be able to understand what we need to prove and do it effectively.