Question

The cuboid water tank has length 2m, breadth 1.6m and height 1.8m. Find the capacity of the tank in liters.

Answer 1

Hint: To solve the question given above, we will first find out what a cuboid is and what its shape is. Then, we will make a rough sketch of cuboid and in that rough sketch, we will mark its length, breadth and height. After doing this, we will find the volume of the cuboid using the formula: \({\rm{Volume = Length}} \times {\rm{breadth}} \times {\rm{height}}{\rm{.}}\) After finding the volume of given cuboid water tank using the conversion \(1{m^3} = 1000{\rm{ liters}}\)

Complete step-by-step answer:
Before we solve the question, we must know what a cuboid is. A cuboid is a three dimensional shape which has 6 rectangular faces and all the faces are perpendicular to their adjacent faces. Now, we will draw a rough sketch of the cuboid water tank to understand the question better.

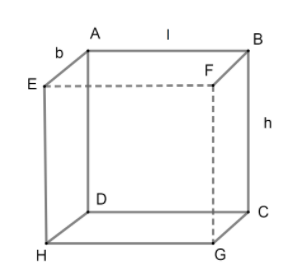
In the above figure, l represents length, b represents breadth and h represents height. Here, we have assumed that, AB is the length, AE is the breadth and BC is the height.
Now, we will find the volume of this cuboid water tank. If a cuboid has length 'x', breadth 'y' and height 'z', then, the volume of this cuboid is giving by:
Volume of cuboid \( = x \times y \times z\)
In our case, \(x = 2m,y = 1.6m{\rm{ and }}z = 1.8m\). Thus, we will get following volume:
Volume of cuboid\( = 2m \times 1.6m \times 1.8m\)
Volume of cuboid\( = \left( {2 \times 1.6 \times 1.8} \right){m^3}\)
Volume of cuboid\( = 5.76{m^3}\)
Thus, the volume of cuboid water tank is \(5.76{m^3}\)
Now, we will find the following conversion for finding out the capacity.
\(1{m^3} = 1000{\rm{ liters}}\)
Thus, we will get:
Capacity\( = 5.76 \times 1000{\rm{ liters}}\)
Capacity\( = 5760{\rm{ liters}}\)
Thus, the capacity of a cuboid water tank is 5760 liters.

Note: We can also proceed in the following way after finding out the volume. We know that, volume \( = 5.76{m^3} \Rightarrow 5.76m \times m \times m \Rightarrow 5.76 \times 100cm \times 100cm \times 100cm.\) Therefore, volume \( = 5760000c{m^3}\).Now, we know that, \(1{\rm{ liter = 1000}}c{m^3}\)
Thus:
Volume \( = 5760 \times 1000c{m^3} \Rightarrow 5760{\rm{ liters}}\).