Question

The current flowing through the resistor in a series LCR a.c. circuit, is $I = \dfrac{\varepsilon }{R}$.
Now the inductor and capacitor are connected in parallel and joined in series with the resistor as shown in figure. The current in the circuit is now. (Symbols have their usual meaning)

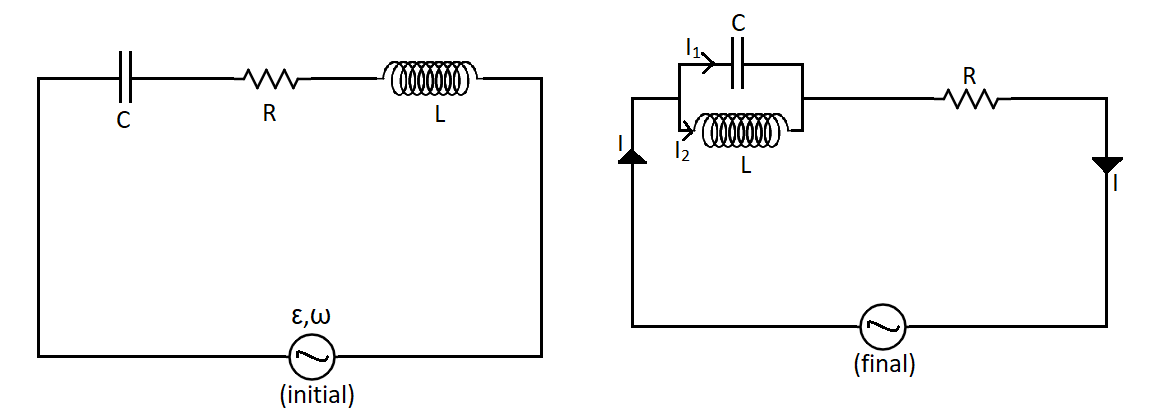
(A) Equal to $I$
(B) More than $I$
(C) Less than $I$
(D) zero

Answer 1

Hint
We need to find the relation between the capacitance, inductance and the frequency using the condition $I = \dfrac{\varepsilon }{R}$ in the first circuit. And then using that condition, find the total impedance in the second circuit. So the current will be given by the emf divided by the impedance.
Formula Used: In this solution, we will be using the following formula,
${X_L} = \omega L$ where ${X_L}$ is impedance across inductor
$\omega $ is frequency and $L$ is inductance.
${X_C} = \dfrac{1}{{\omega C}}$ where ${X_C}$ is impedance across capacitor and $C$ is capacitance.

Complete step by step answer
According to the question, the current through the resistor in the first circuit is given by the formula, $I = \dfrac{\varepsilon }{R}$
So the impedance across the capacitor and the inductor cancel out each other.
Now the impedance across the capacitor is given by,
${X_C} = \dfrac{1}{{\omega C}}$
And that across the inductor is given by,
${X_L} = \omega L$
So equating them we get the frequency of the source as,
$\omega L = \dfrac{1}{{\omega C}}$
On bringing $\omega $ to one side, we get,
${\omega ^2} = \dfrac{1}{{LC}}$
On taking square root on both sides we get,
$\omega = \dfrac{1}{{\sqrt {LC} }}$
In the second case, the capacitor and the inductor are in parallel circuits. So we can calculate the impedance across by the formula for the two parallel resistances. That is,
${X_{eq}} = \dfrac{{{X_C} \times {X_L}}}{{{X_C} + {X_L}}}$
Substituting the values we get,
${X_{eq}} = \dfrac{{\omega L \times \dfrac{1}{{\omega C}}}}{{\omega L - \dfrac{1}{{\omega C}}}}$
In the numerator we can cancel the $\omega $ and in the denominator taking LCM as $\omega C$
${X_{eq}} = \dfrac{{L \times \dfrac{1}{C}}}{{\dfrac{{{\omega ^2}LC - 1}}{{\omega C}}}}$
On simplifying this we get,
${X_{eq}} = \dfrac{{\omega C \times \dfrac{L}{C}}}{{{\omega ^2}CL - 1}} = \dfrac{{L \times \omega }}{{{\omega ^2}CL - 1}}$
Now this is in series with the resistance. So the equivalent impedance in the circuit is given by,
$X = R + \dfrac{{L \times \omega }}{{{\omega ^2}CL - 1}}$
Now, in place of ${\omega ^2}$ we can write ${\omega ^2} = \dfrac{1}{{LC}}$,
Hence, the impedance becomes,
$X = R + \dfrac{{L \times \omega }}{{1 - \dfrac{1}{{LC}}LC}}$
This makes the denominator of the second term zero. Hence we get that second term as infinite.
Therefore, the impedance of the circuit becomes infinite.
So the current in the circuit is given $I = \dfrac{\varepsilon }{X}$
Since the denominator of this fraction is infinite, so the current in the circuit becomes zero.
Therefore the correct answer is option D.

Note
An LCR circuit is also called a resonant circuit or a tuned circuit and it contains a resistor, capacitor, inductor in series or in parallel. Depending on the values of the impedances of an LCR circuit, it has 3 conditions,
- When ${X_L} > {X_C}$ it is inductive circuit
- When ${X_L} < {X_C}$ it is capacitive circuit
- When ${X_L} = {X_C}$ it is a resonant circuit.