Question

The curved surface area of a frustum cone is \[240{\text{ }}c{m^2}\]. The larger circle area is \[50{\text{ }}c{m^2}\]. The total surface area is \[750{\text{ }}c{m^2}.\] Find the smaller circle area of a cone.
A. \[560{\text{ }}c{m^2}\]
B.\[\;460{\text{ }}c{m^2}\]
C. \[660{\text{ }}c{m^2}\]
D. \[760{\text{ }}c{m^2}\]

Answer 1

Hint: We are given the curved surface area of a frustum cone, the larger circle area, and the total surface area, as the total surface area of the frustum is curved surface area plus larger circle area plus smaller circle area, so as we are given all the values we can find the smaller circle area by subtracting larger circle area and curved surface area from the total surface area.

Complete step by step Answer:

Let us draw the figure:

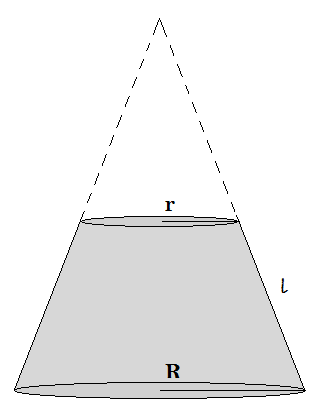
We know that, curved surface area of a frustum cone is given by \[ = \;\pi \left( {R + r} \right)l\;\]
Total surface area of a frustum of cone =\[\pi \left( {R + r} \right)l{\text{ }} + \pi {r^2}\; + \;\pi {R^2}\] 
Larger circle area $ = \;\pi {R^2}\; \Rightarrow \;50{\text{ }}c{m^2}$
We need to find the smaller circle area i.e. \[\pi {r^2}\] 
Now, the curved surface area of a frustum cone is \[240{\text{ }}c{m^2}\].
\[\pi \left( {R + r} \right)l\;\]\[ = 240\]\[c{m^2}\]
Again, the total surface area of a frustum cone is \[750{\text{ }}c{m^2}\].
Therefore,
\[\pi \left( {R + r} \right)l{\text{ }} + \pi {r^2}\; + \;\pi {R^2} = 750c{m^2}\]
Since \[\pi {R^2}\; = \;50{\text{ }}c{m^2}\], we get,
\[ \Rightarrow \pi \left( {R + r} \right)l{\text{ }} + \pi {r^2}\; + \;50 = 750\]
On simplification we get,
\[ \Rightarrow \pi \left( {R + r} \right)l{\text{ }} + \pi {r^2}\; = 700\]
Since \[\pi \left( {R + r} \right)l\; = 240c{m^2}\], we get,
\[ \Rightarrow 240 + \pi {r^2}\; = 700\]
On simplification we get,
\[ \Rightarrow \pi {r^2}\; = 460\]\[c{m^2}\]
Therefore, area of the smaller circle of frustum cone is \[460{\text{ }}c{m^2}\]
Hence option (B) is the correct option.

Note: A frustum cone is formed from a right circular cone by cutting off the tip with a cut perpendicular to the height, forming a lower base and an upper base that are circular and parallel to each other.
Note that,
Curved surface area of a frustum cone is given by \[ = \;\pi \left( {R + r} \right)l\;\]
Total surface area of a frustum of cone = \[\pi \left( {R + r} \right)l{\text{ }} + \pi {r^2}\; + \;\pi {R^2}\]