Question

The curved surface area of a frustum cone is $25\pi m{m^2}$ . The larger circle area is $12\pi m{m^2}$.The total surface area is $350\pi m{m^2}$.Find the smaller circle area of a cone
a.$313m{m^2}$
b.$323\pi m{m^2}$
c.$333\pi m{m^2}$
d.$313\pi m{m^2}$

Answer 1

Hint: We are given the curved surface area , total surface area , the area of the bigger circle and we can use the formula of area of circle $\pi {r^2}sq.units$, curved surface area of frustum $\pi (r + R)h{\text{ }}sq.units$ and obtain the values of ${R^2}{\text{ and }}(R + r)h$ and substitute it in the formula of total surface area of the sphere $\pi [(r + R)h + {r^2} + {R^2}]{\text{ }}sq.units$. After that use the area of the circle formula to get the area of the smaller circle

Complete step-by-step answer:
Let's consider a frustum with height h and smaller radius r and bigger radius R

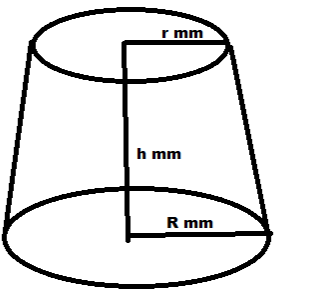
We are given the area of the bigger circle to $12\pi m{m^2}$
We know that the area of circle is given by $\pi {r^2}sq.units$
Therefore
Area of bigger circle $ = \pi {R^2}sq.units$
$
   \Rightarrow 12\pi = \pi {R^2} \\
   \Rightarrow 12 = {R^2} \\
$
Let this be equation (1)
We are given that the curved surface area of the frustum is $25\pi m{m^2}$
We know that the curved surface area of a frustum is given by $\pi (r + R)h{\text{ }}sq.units$
$
   \Rightarrow \pi (r + R)h{\text{ = 25}}\pi \\
   \Rightarrow (r + R)h = 25 \\
$
Let this be equation (2)
We are given that the total surface area is $350\pi m{m^2}$
We know that the total surface area of a frustum is given by $\pi [(r + R)h + {r^2} + {R^2}]{\text{ }}sq.units$
$
   \Rightarrow \pi [(r + R)h + {r^2} + {R^2}]{\text{ = 350}}\pi \\
   \Rightarrow [(r + R)h + {r^2} + {R^2}]{\text{ }} = 350 \\
$
Substitute the values from equation (1) and (2) we get
$
   \Rightarrow (25 + {r^2} + 12) = 350 \\
   \Rightarrow 37 + {r^2} = 350 \\
   \Rightarrow {r^2} = 350 - 37 \\
   \Rightarrow {r^2} = 313 \\
$
We know that the area of circle is given by $\pi {r^2}sq.units$
Therefore
Area of smaller circle $ = \pi {r^2}sq.units = 313\pi m{m^2}$
The correct option is d.

Note: A frustum is the part of a conical solid left after cutting off a top portion with a plane parallel to the base. The part of a solid, as a cone or pyramid, between two usually parallel cutting planes.
Many students tend to make the calculation difficult by substituting the value of $\pi $ and then dividing which consumes a lot of time.