
The curved surface area of a right circular cone of height 15cm and base diameter 16 cm is………………………….
Answer
529.5k+ views
Hint: In this question the height and base diameter of a right circular cone is given. Use the direct formula for curved surface area for the right circular cone (
Complete step-by-step answer:
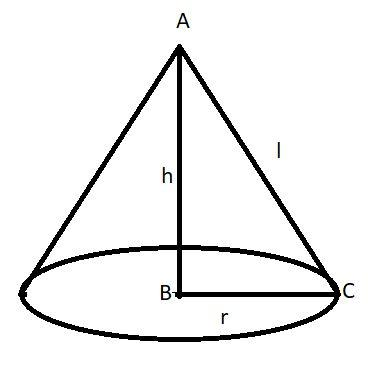
As we know that the curved surface area (C.S.A) of the right circular cone is
Where, l = slant height of the cone.
r = base radius of the cone.
Now it is given that the height (h) of the cone is 15 cm and the diameter (d) of the cone is 16 cm.
Now as we know that the radius (r) is half of the diameter (d).
Now in a right circular cone slant height (l) is given as
In triangle ABC apply Pythagoras theorem we have,
So substitute the value in the above equation we have,
So the curved surface area (C.S.A) of the right circular cone is
So this is the required curved surface area (C.S.A) of a right circular cone.
Hence option (d) is correct.
Note: Whenever we face such types of problems the key point is to have the good gist of the diagrammatic representation using the information provided in the question as it helps understanding the geometry of the figure involved. It is always advisable to learn the direct formula for some of the basic conic sections like the right circular cone as it helps to save a lot of time.
Complete step-by-step answer:

As we know that the curved surface area (C.S.A) of the right circular cone is
Where, l = slant height of the cone.
r = base radius of the cone.
Now it is given that the height (h) of the cone is 15 cm and the diameter (d) of the cone is 16 cm.
Now as we know that the radius (r) is half of the diameter (d).
Now in a right circular cone slant height (l) is given as
In triangle ABC apply Pythagoras theorem we have,
So substitute the value in the above equation we have,
So the curved surface area (C.S.A) of the right circular cone is
So this is the required curved surface area (C.S.A) of a right circular cone.
Hence option (d) is correct.
Note: Whenever we face such types of problems the key point is to have the good gist of the diagrammatic representation using the information provided in the question as it helps understanding the geometry of the figure involved. It is always advisable to learn the direct formula for some of the basic conic sections like the right circular cone as it helps to save a lot of time.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




