Question

The diagonals of a rhombus are 10cm and 24cm. Find the length of each side of a rhombus.

Answer 1

Hint: Let us draw a rough figure as follows

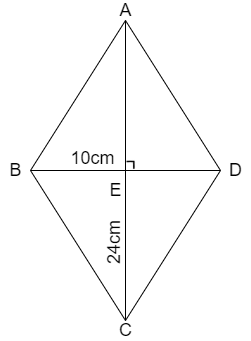
We solve this problem by using the definition of rhombus that is all the sides of rhombus are equal. We also use the condition that the diagonals intersect at right angles at mid – points. For finding the side length we use the Pythagoras Theorem states that the square of hypotenuse is equal to sum of squares of other two sides that is for the triangle shown below

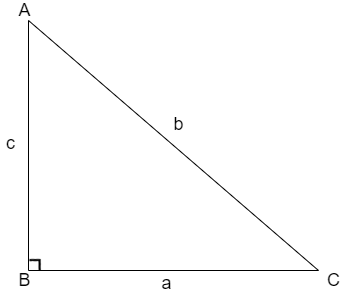
The Pythagoras theorem is given as\[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].

Complete step by step answer:
We are given that the length of diagonals as 10cm and 24cm
Let us assume that from the figure the length of diagonals as
\[\Rightarrow AC=24cm\]
\[\Rightarrow BD=10cm\]
We know that the diagonals of rhombus intersect at right angles at mid – points that means the point ‘E’ is mid – point of both ‘AC’ and ‘BD’
By using the above condition the length of ED can be calculated as
\[\Rightarrow ED=\dfrac{BD}{2}\]
By substituting the required values we get
\[\Rightarrow ED=\dfrac{10cm}{2}=5cm\]
 Similarly, by using the condition that point ‘E’ is mid – point of ‘AC’ we get
\[\Rightarrow AE=\dfrac{AC}{2}\]
By substituting the required values we get
\[\Rightarrow AE=\dfrac{24cm}{2}=12cm\]
Now, let us consider the triangle \[\Delta AED\]
We know that the Pythagoras Theorem states that the square of hypotenuse is equal to sum of squares of other two sides that is for the triangle shown below

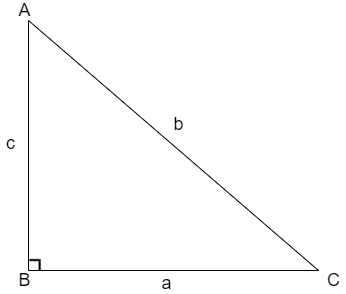
The Pythagoras theorem is given as\[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].
By using the Pythagoras theorem to triangle \[\Delta AED\] we get
\[\Rightarrow A{{D}^{2}}=A{{E}^{2}}+E{{D}^{2}}\]
By substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow A{{D}^{2}}={{5}^{2}}+{{12}^{2}} \\
 & \Rightarrow A{{D}^{2}}=25+144 \\
 & \Rightarrow AD=\sqrt{169}=13cm \\
\end{align}\]
We know that all the sides of a rhombus are equal
By using the above condition we get
\[\Rightarrow AB=AC=CD=DA=13cm\]

Therefore the length of each side of a given rhombus is 13cm.

Note: We can solve this problem in another method.
If \[p,q\] are lengths of diagonals of a rhombus then the area is given as
\[\Rightarrow A=\dfrac{1}{2}\times p\times q\]
If \[p\] is length of diagonal and \[a\] is side length of rhombus the area formula is given as
\[\Rightarrow A=\dfrac{1}{2}\times p\times \sqrt{4{{a}^{2}}-{{p}^{2}}}\]
Since the area will be same in any method by equating them we get
\[\begin{align}
  & \Rightarrow \dfrac{1}{2}\times p\times q=\dfrac{1}{2}\times p\times \sqrt{4{{a}^{2}}-{{p}^{2}}} \\
 & \Rightarrow q=\sqrt{4{{a}^{2}}-{{p}^{2}}} \\
\end{align}\]
Now by squaring on both sides we get
\[\Rightarrow 4{{a}^{2}}={{p}^{2}}+{{q}^{2}}\]
Now, by substituting the required values we get
\[\begin{align}
  & \Rightarrow 4{{a}^{2}}={{10}^{2}}+{{12}^{2}} \\
 & \Rightarrow {{a}^{2}}=\dfrac{100+144}{4} \\
 & \Rightarrow a=\sqrt{169}=13cm \\
\end{align}\]
Therefore the length of each side of a given rhombus is 13cm.