Question

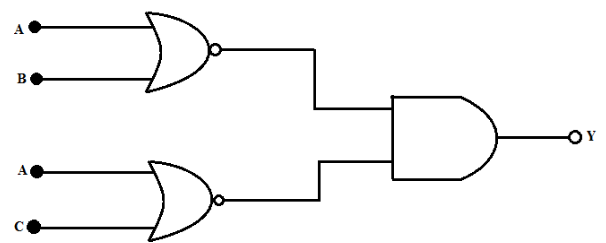
The diagram of the logic gate circuit is given below. The output Y of the circuit is represented by

(A) \[A \cdot \left( {B + C} \right)\]
(B) \[A \cdot \left( {B \cdot C} \right)\]
(C) \[A + \left( {B \cdot C} \right)\]
(D) \[A + \left( {B + C} \right)\]

Answer 1

Hint: In the above logic gate, the output of two or gates is given to the input of AND gate. Use laws of boolean algebra to simplify the boolean expression. Use annulment law which gives, \[1 + C = 1\].

Complete step by step answer:
We can see in the above logic gate circuit, the output of both the OR gates is given to the input of AND gate.

We know the output of an OR gate is the sum of inputs. Therefore, the output of upper OR gate is,
\[{Y_1} = A + B\]

Also, the output of lower OR gate is,
\[{Y_2} = A + C\]
Now, we know that the output of the AND gate is the multiplication of the inputs. Therefore, we can write the output of AND gate as,
\[Y = {Y_1} \cdot {Y_2}\]
\[ \Rightarrow Y = \left( {A + B} \right) \cdot \left( {A + C} \right)\]
\[ \Rightarrow Y = A \cdot A + A \cdot C + A \cdot B + B \cdot C\]
We know the identity, \[A \cdot A = A\]. Therefore, the above Boolean expression becomes,
\[Y = A + A \cdot C + A \cdot B + B \cdot C\]
\[ \Rightarrow Y = A\left( {1 + C} \right) + A \cdot B + B \cdot C\]
We know the identity, \[1 + C = 1\]. Therefore, the above Boolean expression becomes,
\[Y = A + A \cdot B + B \cdot C\]
\[ \Rightarrow Y = A\left( {1 + B} \right) + B \cdot C\]
\[ \therefore Y = A + B \cdot C\]

So, the correct answer is option (C).

Additional information:
We will explain the laws of Boolean algebra in brief as follows.
Commutative law: On interchanging of two operands for the output of OR and AND gate does not change the results. For example, \[A + B = B + A\] and \[A \cdot B = B \cdot A\].
Distributive law: According to distributive law, if we multiply the two variables and add another variable to it, the result will be the multiplication of addition of the individual variables. For example, \[A + BC = \left( {A + B} \right)\left( {A + C} \right)\].

Note:While solving these types of questions, students should remember all the boolean laws for the simplification of the boolean expression. Students should also remember De Morgan’s law if the NOT gate is present in the logic circuit. In the solution, we have used commutative law to write \[B \cdot A = A \cdot B\].