
The diagram shows a trapezium
Answer
441k+ views
Hint: As we know that a trapezium is a quadrilateral having two parallel sides of unequal length and the other two sides are non- parallel. The parallel sides of a trapezium are called bases and the non parallel sides are called the legs. The area of the trapezium is
Complete step by step solution:
First we will draw the diagram according to the questions:
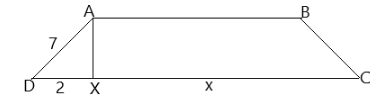
In the above figure we can see that
We have
It gives us the value
We have been given that the area of the trapezium is
So we can write
We will solve it now by isolating the term
Therefore:
Taking the common factor out
Hence the required answer is
So, the correct answer is “
Note: Before solving this kind of question we should know all the properties and the formulas of the trapezium. We should note that the question says that the AX is perpendicular so that makes the angle
Complete step by step solution:
First we will draw the diagram according to the questions:

In the above figure we can see that
We have
It gives us the value
We have been given that the area of the trapezium is
So we can write
We will solve it now by isolating the term
Therefore:
Taking the common factor out
Hence the required answer is
So, the correct answer is “
Note: Before solving this kind of question we should know all the properties and the formulas of the trapezium. We should note that the question says that the AX is perpendicular so that makes the angle
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




