Question

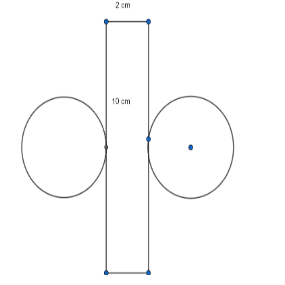
The diagram shows the net of the right cylinder. Find the volume of cylinder, in \[c{{m}^{3}}\].

\[\begin{align}
  & (A)\text{ }\dfrac{20}{\pi } \\
 & (B)\text{ }\dfrac{50}{\pi } \\
 & (C)\text{ }\dfrac{25}{\pi } \\
 & (D)\text{ 40}\pi \\
\end{align}\]

Answer 1

Hint: To find the volume of the cylinder, first we have to roll the given diagram over a plane. We get the height of the cylinder as 10 cm and circumference of the cylinder as 2cm. Now, we can apply the formula for volume of cylinder \[V=\pi {{r}^{2}}h\].

Complete step-by-step answer:
From the given diagram it is clear that the length of the net of the right cylinder is 10 cm and the breadth of the net of the right cylinder is 2cm.

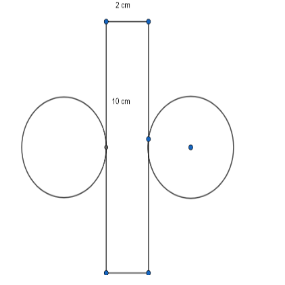
Initially, we have to form a cylinder with the given diagram.
To form a cylinder with a given diagram, lift the circle at the right angle from the present position. Now roll the rectangle over the two circles
After completing the rolling of the net of the right cylinder, the resultant cylinder appears as follows.
 

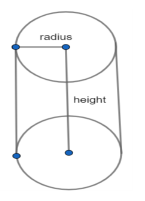
After rolling the net of the right circular cylinder, we can observe that the circumference of the cylinder at its ends is equal to the length of the rectangle in the net of the cylinder.
We can also observe that the breadth of the net of the right circular cylinder is equal to the height of the right circular cylinder.
From the given question, we know that the length of the net of the right circular cylinder is 10 cm and the breadth of the net of the right circular cylinder is equal to 2cm.
So, the circumference of the cylinder at its ends is equal to 10 cm and the height of the cylinder at its ends is equal to 2 cm.
Assume the radius of the cylinder as r cm.
We know the formula for circumference of a circle.
Circumference of circle = \[2\pi r\]
\[\Rightarrow 10=2\pi r.....(1)\]
We should divide equation (1) with \[2\pi \].
\[\Rightarrow r=\dfrac{5}{\pi }......(2)\]
Assume the height of the cylinder as h.
\[\Rightarrow h=2......(3)\]
We know the formulae of volume of cylinder \[V=\pi {{r}^{2}}h.......(4)\]
Substitute equation (2) and equation (3) in equation (4).
\[\Rightarrow V=\pi {{\left( \dfrac{5}{\pi } \right)}^{2}}\left( 2 \right)\]
\[\Rightarrow V=\pi \left( \dfrac{25}{{{\pi }^{2}}} \right)\left( 2 \right)\]
\[\Rightarrow V=\dfrac{50}{\pi }\]
Hence, option (A) is correct.

Note:

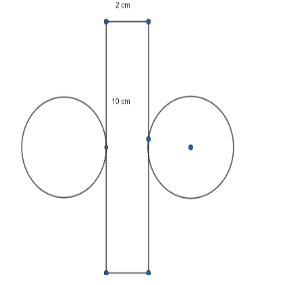
We should be careful while noting the circumference of cylinder and height of cylinder from the net of the cylinder. Students may get confused while considering the values for circumference and height of the cylinder. Students may misinterpret and consider the value of circumference as 2 cm and height of cylinder as 10 cm. So, we should remember that the length of the side of a rectangle having circles in the net of the cylinder represent circumference of the base of the cylinder. The length of the side of the rectangle in the net of the cylinder not having circles represents the height of the cylinder.