Question

The direction ratios of normal to the plane through the points \[(0,-1,0)\] and \[(0,0,1)\] and making an angle \[\dfrac{\pi }{4}\] with the plane \[y-z+5=0\] is?
A. \[2\sqrt{3},1,-1\]
B. $2,\sqrt{2},\sqrt{2}$
C. $2,-1,1$
D. $\sqrt{2},1,-1$

Answer 1

Hint: We must start with general equation of a plane which is given as $ax+by+cz+d=0$ that satisfies above two points since it passes through them, This gives us two equations in \[a\],\[b\],\[c\],\[d\] which on subtracting from each other eliminates the unknown constant \[d\] and dot product \[\overrightarrow{A}\centerdot \overrightarrow{B}\] of direction vectors of two planes must be used in order to obtain second equation.

Complete step by step answer:
We start with the general equation of a plane $ax+by+cz+d=0$ and $\vec{p}=\left\langle a,b,c \right\rangle $ where \[\overrightarrow{p}\] is direction number in the direction of normal to the plane. As per question, the plane must pass through the points \[(0,-1,0)\] and \[(0,0,1)\].
First, we focus on the first part of the question. The plane passes through two points \[(0,-1,0)\] & \[(0,0,1)\] and must satisfy the above general equation of the plane. Putting the given two points in the equation of the plane we get two equations.
\[a(0)+b(-1)+c(0)+d=0\ldots eq(1)\]
\[a(0)+b(0)+c(1)+d=0\ldots eq(2)\]
Subtracting $eq(1)$ from $eq(2)$,
\[b+c=0\ldots eq(3)\]

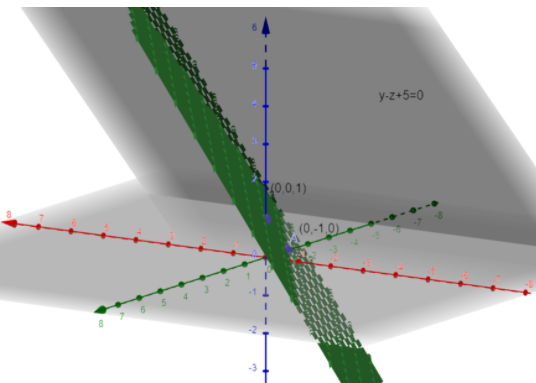
Now we focus on the second part of the question. The given direction vector \[\overrightarrow{p}\] makes \[\dfrac{\pi }{4}\] with the normal of plane \[y-z+5=0\], whose direction vector is \[\overrightarrow{a}=\left\langle 0,1,-1 \right\rangle \]. So the angle between the direction vector and the normal of the plane $y-z+5=0$ is \[\dfrac{\pi }{4}\] radian.
$\vec{a}\centerdot \vec{b}=\left| a \right|\left| b \right|\cos \theta $, where Ѳ is the angle between vectors a and b
$\left\langle 0,1,-1 \right\rangle \centerdot \left\langle a,b,c \right\rangle =\sqrt{2}\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}cos\dfrac{\pi }{4}$
 $(b-c)=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}$
Squaring both sides and solving, we get
${{a}^{{{2}^{{}}}}}=-2bc\ldots eq(4)$
Using eq(3) and eq(4) ,
${{a}^{2}}=2{{b}^{2}}$
$b=\pm \dfrac{a}{\sqrt{2}},c=\mp \dfrac{a}{\sqrt{2}}$
Hence, \[\vec{p}=a\left\langle 1,\pm \dfrac{1}{\sqrt{2}},\mp \dfrac{1}{\sqrt{2}} \right\rangle \]
$a:b:c=\sqrt{2}:\pm 1:\mp 1$
Taking b to be positive, c becomes negative.
Therefore the direction ratio becomes $a:b:c=\sqrt{2}:1:-1$

So, the correct answer is “Option D”.

Note: In above solution there are two equations and three unknown, so two variables must be expressed in terms of third in order to obtain the direction vector. The student take care that he uses dot product \[\overrightarrow{A}\centerdot \overrightarrow{B}\] and not \[\overrightarrow{A}\times \overrightarrow{B}\] otherwise he will find equation of line perpendicular to plane containing the two lines.