Question

The edge length of a face-centered cubic cell of an ionic substance is $\text{ 508 pm }$. If the radius of the cation is $\text{ 110 pm }$, the radius (in pm) of the anion is:
A) 288
B) 398
C) 618
D) 144

Answer 1

Hint: for face centred cubic (FCC) structure, if the cation is at the corners of the structure and anion at the centre of the face or vice versa, then the relation between the radius of ions and the edge length is stated as follows,
$\text{ 2 }{{\text{r}}^{\text{+}}}\text{ + 2 }{{\text{r}}^{-}}\text{ = }a\text{ }$
Where, $\text{ }{{\text{r}}^{\text{+}}}\text{ }$ is the radius of cation, $\text{ }{{\text{r}}^{-}}\text{ }$is the radius of anion and ‘a’ is the edge length.

Complete step by step solution:
In face centred cubic (FCC) structure, 8 atoms are at the 8 corners of the cubic structure and 6 atoms are at the 6 faces of the structure. The cross-section of the FCC use is as shown below,

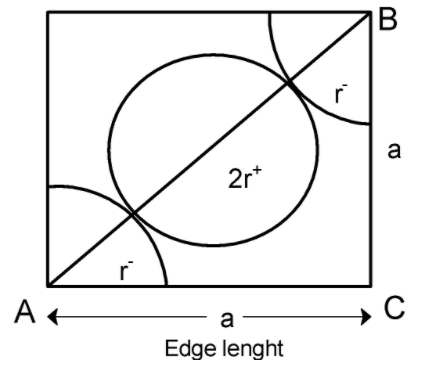
Each face is tightly packed with corner atoms. Atoms have a radius equal to ‘r’.If seen diagonally , one complete atom and two-parts of an atom are situated at the diagonal.
Let's consider that, the anion is at the corners of the cubic structure and the cation is at the centre of the face. Then the face diagonal having a length a is equal to twice the sum of radius of cation and anion.
That is the formula which related the radius of cation, the radius of the anion with the edge length,
$\text{ 2 }{{\text{r}}^{\text{+}}}\text{ + 2 }{{\text{r}}^{-}}\text{ = }a\text{ }$ (1)
Where, $\text{ }{{\text{r}}^{\text{+}}}\text{ }$ is the radius of cation, $\text{ }{{\text{r}}^{-}}\text{ }$is the radius of anion and ‘a’ is the edge length.
 Here we are given with,
Edge length of the FCC cell is, $\text{ 508 pm }$
The radius of the cation is given as, $\text{ 110 pm }$
We are interested to find the radius of the anion.
Let's substitute the values in the above equation (1). we have,
$\begin{align}
& \text{ 2 }{{\text{r}}^{\text{+}}}\text{ + 2 }{{\text{r}}^{-}}\text{ = }a\text{ } \\
& \Rightarrow {{\text{r}}^{-}}\text{ = }\frac{a-\text{2 }{{\text{r}}^{\text{+}}}}{2} \\
& \Rightarrow {{\text{r}}^{-}}\text{ = }\frac{508-\text{2 }\left( 110 \right)}{2} \\
& \therefore {{\text{r}}^{-}}\text{ = 144 pm } \\
\end{align}$
Therefore, the radius of the anion is equal to 144 pm.

Hence, (D) is the correct option.

Note: It is important to note that the value of the ionic radii obtained from the edge length of the unit cell depends on the numerous assumptions. Such as, the perfect sphere shape of ions. Hence, the values are always approximate and can be further calculated by x-ray crystallography.