Question

The electric dipole moment of an HCl atom is $3.4 \times 10^{-30}\;Cm$. The charges on both atoms are unlike and of the same magnitude. Magnitude of this charge is ______. The distance between the charges is 0.1nm.
A. $1.7 \times 10^{-20}\;C$
B. $3.4 \times 10^{-20}\;C$
C. $6.8 \times 10^{-20}\;C$
D. $3.4 \times 10^{-10}\;C$

Answer 1

Hint: Recall that the dipole moment between the H and the Cl atoms arises because of the difference in electronegativity of the two atoms. This dipole moment is thus proportional to the charge on the atoms and the distance between them. Use this relation to substitute the values given to us and to subsequently arrive at the appropriate solution.
Formula Used: Dipole moment $\mu = \delta .d$

Complete step-by-step solution:
Let us begin by understanding what the dipole moment is.
Separation of charges in any system gives rise to a dipole moment. Separation of charges occurs on the atomic or molecular scales, for example, in the formation of ionic and covalent bonds between the atoms of a molecule. The difference in the electronegativity between the two atoms participating in a chemical bond leads to the development of a dipole moment between them.
The dipole moment basically measures the polarity or the separation between two atoms in a molecule or the separation of negative and positive charges in a system. If the participating atoms are not like-charged then the resultant bond dipole moment will be an electric dipole moment. This dipole moment is a vector quantity and has both magnitude and direction.

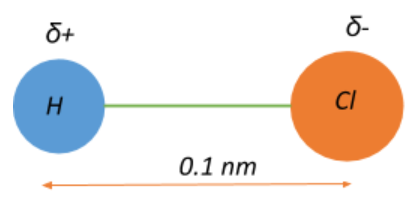
Thus, the electric dipole moment is the bond dipole moment that arises from the difference in the electronegativities of the chemically bound atoms in a molecule, and it can be quantified as:
$\mu = \delta.d$, where $\mu$ is the dipole moment, $\delta$ is the magnitude of the partial charges $\delta +$ and $\delta -$, and d is the distance between the two atoms.
Given that $\mu = 3.4 \times 10^{-30}\;Cm$ and $d = 0.1\;nm = 10^{-10}\;m$
$\Rightarrow 3.4 \times 10^{-30} = \delta . 10^{-10} \Rightarrow \delta = \dfrac{3.4 \times 10^{-30}}{10^{-10}} = 3.4\times 10^{-30+10} = 3.4 \times 10^{-20}\;C$
Therefore, the correct choice would be B. $3.4 \times 10^{-20}\;C$

Note: Remember that what actually happens in bringing about a dipole moment is that when two atoms with different electronegativities interact, the electrons move from their positions to come closer to the relatively more electronegative tom. This movement is what characterizes the dipole moment.
Another easy way to remember what dipole moment means is to use an analogy with the theory of moments which states that for an object to be balanced, the sum of clockwise moments should be equal to the sum of anticlockwise moments about a pivot. Thus, moments define the range of motion, just like how dipole moment defines the molecule’s range of motion.