
The equation of common tangent to the parabola
Answer
521.4k+ views
Hint: In this question
Complete step-by-step answer:
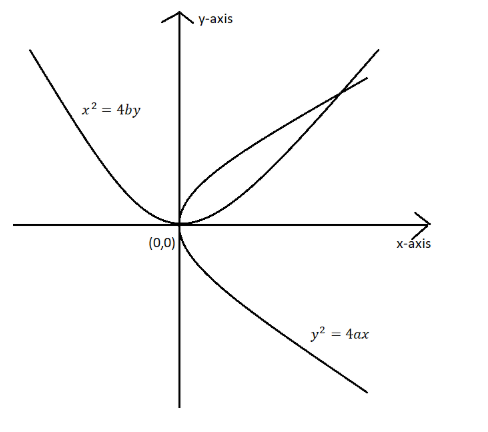
We know equation of tangent to parabola to
And the equation of tangent to parabola to
For common tangent, eq.1 and eq.2 represent the same line. Therefore, the same slope and the same y-intercept.
Now considering eq.4 using relation of eq.3, we get
Now, put value of
Now on rearranging the terms of above equation to get answer in form of given options
Using property
We can rewrite above equation as
Now using property
Hence, option A. is correct.
Note: Whenever you get this type of question the key concept to solve this is to learn equation of tangents of different curves in different conditions like in this question we require tangent of parabola in different scenario(
Complete step-by-step answer:

We know equation of tangent to parabola to
And the equation of tangent to parabola to
For common tangent, eq.1 and eq.2 represent the same line. Therefore, the same slope and the same y-intercept.
Now considering eq.4 using relation of eq.3, we get
Now, put value of
Now on rearranging the terms of above equation to get answer in form of given options
Using property
We can rewrite above equation as
Now using property
Hence, option A. is correct.
Note: Whenever you get this type of question the key concept to solve this is to learn equation of tangents of different curves in different conditions like in this question we require tangent of parabola in different scenario(
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Franz thinks Will they make them sing in German even class 12 english CBSE




